题目内容
【题目】如图,正方形ABCD和四边形ACEF所在的平面互相垂直.EF∥AC,AB= ![]() ,CE=EF=1. (Ⅰ)求证:AF∥平面BDE;
,CE=EF=1. (Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE.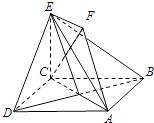
【答案】证明:(Ⅰ)设AC于BD交于点G. 因为EF∥AG,且EF=1,AG= ![]() AC=1,
AC=1,
所以四边形AGEF为平行四边形,
所以AF∥EG,
因为EG平面BDE,AF平面BDE,
所以AF∥平面BDE.
(Ⅱ)连接FG.因为EF∥CG,EF=CG=1,
且CE=1,所以平行四边形CEFG为菱形.所以CF⊥EG.
因为四边形ABCD为正方形,所以BD⊥AC.
又因为平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,
所以BD⊥平面ACEF.
所以CF⊥BD.又BD∩EG=G,
所以CF⊥平面BDE.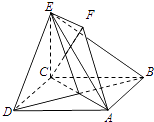
【解析】(Ⅰ)证明平面BDE外的直线AF平行平面BDE内的直线GE,即可证明AF∥平面BDE;(Ⅱ)证明CF垂直平面BDF内的两条相交直线:BD、EG,即可证明求CF⊥平面BDF;
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对直线与平面垂直的判定的理解,了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目