题目内容
【题目】已知数列{an}的首项为1，前n项和Sn与an之间满足an= 
（n≥2，n∈N*）
（1）求证：数列{ 
}是等差数列；
（2）求数列{an}的通项公式；
（3）设存在正整数k，使（1+S1）（1+S1）…（1+Sn）≥k 
对于一切n∈N*都成立，求k的最大值．
【答案】
（1）证明：∵数列{an}的前n项和Sn与an之间满足an= 
（n≥2，n∈N*），
∴Sn﹣Sn﹣1= ，化为： 
﹣ 
=2．
∴数列{ }是等差数列，公差为2，首项为1．
（2）解：由（1）可得： =1+2（n﹣1）=2n﹣1，可得Sn= 
．
∴n≥2时，an=Sn﹣Sn﹣1= ﹣ 
．
∴an=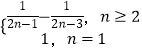 
．
（3）解：∵1+Sn=1+ = 
．
∴Tn=（1+S1）（1+S1）…（1+Sn）= 
× 
×…× ＞ 
× 
×…× 
= 
×…× 
×（2n+1）
= 
，
可得：Tn＞ 
．
∴存在正整数k，使（1+S1）（1+S1）…（1+Sn）≥k 对于一切n∈N*都成立，则k的最大值为1．
【解析】（1）数列{an}的前n项和Sn与an之间满足an= （n≥2，n∈N*），可得Sn﹣Sn﹣1= ，化为： ﹣ =2．即可证明．（2）由（1）可得： =1+2（n﹣1）=2n﹣1，可得Sn= ．n≥2时，an=Sn﹣Sn﹣1；n=1时，a1=1．（3）1+Sn=1+ = ．可得Tn=（1+S1）（1+S1）…（1+Sn）= × ×…× ＞ × ×…× = ×…× ×（2n+1）= ，可得：Tn＞ ．即可得出．
【题目】某货运员拟运送甲、乙两种货物，每件货物的体积、重量、可获利润如表所示：
体积（升/件） | 重量（公斤/件） | 利润（元/件） | |
甲 | 20 | 10 | 8 |
乙 | 10 | 20 | 10 |
在一次运输中，货物总体积不超过110升，总重量不超过100公斤，那么在合理的安排下，一次运输获得的最大利润为（ ）
A.65元
B.62元
C.60元
D.56元
【题目】某市为了解本市2万名学生的汉字书写水平，在全市范围内进行了汉字听写考试，现从某校随机抽取了50名学生，将所得成绩整理后，发现其成绩全部介于
之间，将其成绩按如下分成六组，得到频数分布表
成绩 |
|
|
|
|
|
|
人数 | 4 | 10 | 16 | 10 | 6 | 4 |
（1）在答题卡上作出这些数据的频率分布直方图；
（2）估算该校50名学生成绩的平均值
和中位数（同一组中的数据用该组区间的中点值作代表）；
（3）以该校50名学生成绩的频率作为概率，试估计该市分数在
的人数.
