题目内容
【题目】如图,已知直三棱柱ABC﹣A1B1C1 , 点P、Q分别在棱AA1和CC1上,AP=C1Q,则平面BPQ把三棱柱分成两部分的体积比为( ) 
A.2:1
B.3:1
C.3:2
D.4:3
【答案】A
【解析】解:设直三棱柱ABC﹣A1B1C1的体积为V,∵连接BA1 , BC1 , 点P、Q分别在棱AA1和CC1上,AP=C1Q,
∴四棱锥的B﹣APQC,B﹣C1QPA1 , 的底面积相等
∴把直三棱柱ABC﹣A1B1C1分割为:B﹣APQC,B﹣C1QPA1 , B﹣B1A1C1 ,
∴三棱锥的B﹣B1A1C1为 ![]() V,
V,
∴四棱锥B﹣APQC,B﹣C1QPA1的体积之和为:V﹣ ![]() V=
V= ![]() ,
,
∵四棱锥的B﹣APQC,B﹣C1QPA1 , 的底面积,高相等.
∴四棱锥的B﹣APQC,B﹣C1QPA1 , 的体积相等,
即为 ![]() ,
,
∴棱锥B﹣APQC,B﹣C1QPA1 , B﹣B1A1C1的体积相等,为 ![]() ,
,
∴平面BPQ把三棱柱分成两部分的体积比为2:1,
故选:A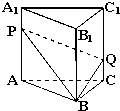

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目