题目内容
求两条渐近线为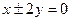
且截直线
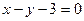所得弦长为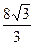
的双曲线方程。
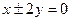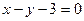且截直线所得弦长为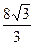的双曲线方程。双曲线方程是：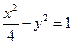
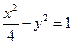
设双曲线方程为x2-4y2=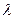
.
联立方程组得: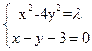
,消去y得，3x2-24x+(36+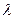)=0
设直线被双曲线截得的弦为AB，且A(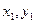
),B(
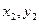)，那么：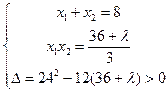
那么：|AB|=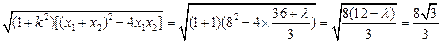
解得: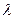=4,所以，所求双曲线方程是：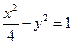
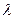.联立方程组得:
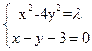,消去y得，3x2-24x+(36+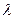)=0设直线被双曲线截得的弦为AB，且A(
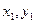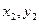),B()，那么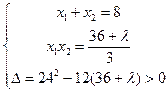： 那么：|AB|=
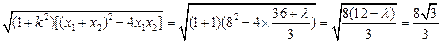
解得:
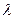=4,所以，所求双曲线方程是：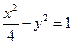
练习册系列答案
相关题目
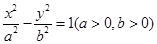的两条渐近线方程为
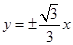，若顶点到渐近线的距离为1，则双曲线方程为 ．
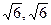），且以直线x= 1为右准线．
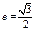且椭圆经过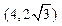
；（2）渐近线方程是
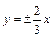，经过点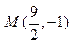
。
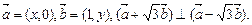
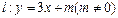与曲线C交于A，B两点，D（0，－1）且有|AD|=|BD|，试求m的值.
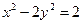的左、右两个焦点为
, 
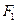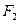，动点P满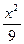
-
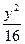=1的两个焦点为F1、F2,点P在双曲线上,若PF1⊥PF2,则点P到x轴的距离为__________________.
=
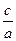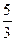，则此双曲线的方程是 ( )
-
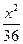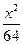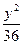="1"
-
=1