题目内容
底面半径为1,高为
的圆锥,其内接圆柱的底面半径为R,内接圆柱的体积最大时R值为______.
| 3 |
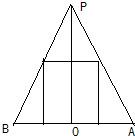
设所求的圆柱的高为h,它的轴截面如图:
由图得,
=
,所以h=
-
R
∴V=πR2(
-
R),V′=2
πR-3
πR2.令V′=0,得R=
得R=
是极大值点,也是最大值点,即当R=
时,内接圆柱的体积最大
故答案为:
由图得,
| ||
|
| R |
| 1 |
| 3 |
| 3 |
∴V=πR2(
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
得R=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |


练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目