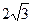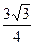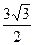题目内容

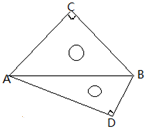
已知球的直径PQ=4，A、B、C是该球球面上的三点，△ABC是正三角形．∠APQ=∠BPQ=∠CPQ=30°，则棱锥P-ABC的体积为（　　）
A．
3
4
3
B．
9
4
3
C．
3
2
3
D．
27
4
3
设球心为M，三角形ABC截面小圆的圆心为0，
∵ABC是等边三角形，∠APQ=∠BPQ=∠CPQ=30°
∴P在面ABC的投影O是等边△ABC的重心（此时四心合一）
∵PQ是直径，
∴∠PCQ=90°．
∴PC=4cos30°=2
3
，
∴PO=2
3
•cos30°=3．
OC=2
3
sin30°=
3

O是等边△ABC的重心
∴OC=
2
3
OH
∴等边三角形ABC的高OH=
3
3
2
，
AC=
3
3
2
sin60°=3．
三棱锥P-ABC体积=
1
3
PO•S△ABC=
1
3
×3×
1
2
×
3
3
2
×3=
9
3
4
．
故选：B．
练习册系列答案
相关题目
如图：先将等腰Rt△ABC的斜边与有一个角为30°的Rt△ADB的斜边重合，然后将等腰Rt△ABC沿着斜边AB翻折成三棱锥C-ABD，若AB=2，则VC-ABD的最大值为______．
如图所示，等腰△ABC的底边AB=6
6
，高CD=3，点E是线段BD上异于点B，D的动点，点F在BC边上，且EF⊥AB，现沿EF将△BEF折起到△PEF的位置，使PE⊥AC，记BE=x，V（x）表示四棱锥P-ACFE的体积．
（1）求V（x）的表达式；
（2）当x为何值时，V（x）取得最大值？
（3）当V（x）取得最大值时，求异面直线AC与PF所成角的余弦值．
底面半径为1，高为
3
的圆锥，其内接圆柱的底面半径为R，内接圆柱的体积最大时R值为______．
一个圆锥高h为3
3
，侧面展开图是个半圆，求：
（1）其母线l与底面半径r之比；
（2）锥角∠BAC；
（3）圆锥的表面积．
一个简单多面体的直观图和三视图如图所示，它的主视图和侧视图都是腰长为1的等腰直角三角形，俯视图为正方形，E是PD的中点．
（Ⅰ）求证：PB∥平面ACE；
（Ⅱ）求证：PC⊥BD；
（Ⅲ）求三棱锥C-PAB的体积．
如图，DA⊥平面ABC，BC⊥AC，E、F分别为BD与CD的中点，DA=AC=BC=2．
（1）证明：EF∥平面ABC；
（2）证明：EF⊥平面DAC；
（3）求三棱锥D-AEF的体积．
直三棱柱ABC-A1B1C1的六个顶点都在球O的球面上．若AB=BC=2，∠ABC=90°，AA1=2
2
，则球O的表面积为______．
某个几何体的三视图如图所示，则该几何体的体积是            （   ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网