题目内容
15.设函数y=$\frac{1}{\sqrt{\frac{9}{x+4}-1}}$的定义域为集合A,集合B={x||x-3|<a,x∈R},其中a∈R.(1)若a=4,求B∩∁UA;
(2)若A∩B=B,求实数a的取值范围.
分析 (1)分别求出求出集合A、B,根据交集和补集的即可求出答案.
(2)由A∩B=B,得到B⊆A,分a≤0时,B=∅,满足B⊆A,a>0,两种情况讨论,分别由子集的关系列出不等式求出a的范围.
解答 解:(1)y=$\frac{1}{\sqrt{\frac{9}{x+4}-1}}$的定义域为集合A,
∴$\frac{9}{x+4}$-1>0,
解得-4<x<5,
∴A=(-4,5),
∴∁UA=(-∞,-4]∪[5,+∞),
当a=4时,|x-3|<4,解得-1<x<7,
∴B=(-1,7),
∴B∩∁UA=[5,7);
(2)∵A∩B=B,
∴B⊆A,
当a≤0时,B=∅,满足B⊆A,
当a>0,|x-3|<a,解得-a+3<x<a+3,
∴B=(-a+3,a+3),
∴$\left\{\begin{array}{l}{-a+3≥-4}\\{a+3≤5}\end{array}\right.$,
解得0<a≤2,
综上所述a的取值范围为(-∞,2].
点评 本题考查了交、并、补集的混合运算,利用集合之间的关系、分类讨论思想求参数的范围,以及一元二不等式的解法.

练习册系列答案
相关题目
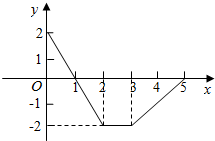 已知y=f(x)的图象如图所示.
已知y=f(x)的图象如图所示.