题目内容
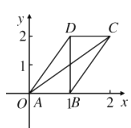
【题目】如图,在圆内接等腰梯形![]() 中,已知
中,已知![]() ,对角线
,对角线![]() 、
、![]() 交于点
交于点![]() ,且图中各条线段长均为正整数,
,且图中各条线段长均为正整数,![]() ,圆的半径
,圆的半径![]() .
.
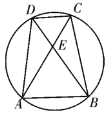
(1)求证:图中存在一个三角形,其三边长均为质数且组成等差数列;
(2)若给图中的线(包括圆、梯形、梯形的对角线)作点染色,使![]() 、
、![]() 、
、![]() 染上红色,其他点染上红蓝色之一,求证:图中存在三个同色点,两两距离相等且长度为质数.
染上红色,其他点染上红蓝色之一,求证:图中存在三个同色点,两两距离相等且长度为质数.
【答案】(1)见解析;(2)见解析
【解析】
(1)在![]() 中,
中,![]() ,外接圆半径为
,外接圆半径为![]() .由正弦定理得
.由正弦定理得
![]() .
.
在![]() 中,由
中,由![]() ,
,![]() ,知
,知![]() 为最长边.故
为最长边.故![]() 、
、![]() 只能取
只能取![]() 之间的整数,即
之间的整数,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
在![]() 中,应用余弦定理得
中,应用余弦定理得![]()
![]() .
.
把![]() 、
、![]() 的可能取值代入验证知
的可能取值代入验证知![]() 、
、![]() 只能取3、5.故存在
只能取3、5.故存在![]() ,其三边长3、5、7均为质数,且组成一个公差为2的等差数列.
,其三边长3、5、7均为质数,且组成一个公差为2的等差数列.
(2)在圆内接等腰梯形中,对![]() 用外角定理、圆周角定理得
用外角定理、圆周角定理得
![]()
![]() .
.
从而,![]() 、
、![]() 均为正三角形.
均为正三角形.
又由![]() ,有
,有![]() .
.
故![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() ,
,![]() 是边长为3的正三角形,
是边长为3的正三角形,![]() 是边长为5的正三角形.
是边长为5的正三角形.
以![]() 为底边作等腰
为底边作等腰![]() .
.
由![]() ,知
,知![]() 是边长为7的正三角形.
是边长为7的正三角形.
同理,可作边长为7的正![]() .
.
如图,联结![]() 交
交![]() 于点
于点![]() ,再联结
,再联结![]() 、
、![]() 、
、![]() .易得
.易得![]() .
.
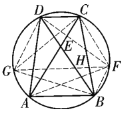
从而,![]()
![]()
![]()
从而,![]() .
.
又![]() ,得
,得![]() 是边长为3的正三角形.
是边长为3的正三角形.
进而,![]() ,
,![]() ,
,
![]() 是边长为
是边长为![]() 的正三角形.
的正三角形.
当![]() 、
、![]() 、
、![]() 中有红点时,
中有红点时,![]() 、
、![]() 、
、![]() 中存在三顶点同为红色的正三角形,其边长为质数3、5、7之一,命题已成立.
中存在三顶点同为红色的正三角形,其边长为质数3、5、7之一,命题已成立.
当![]() 、
、![]() 、
、![]() 中无一为红点时,考虑点
中无一为红点时,考虑点![]() .
.
(1)![]() 为蓝点,则
为蓝点,则![]() 是三顶点同为蓝色的正三角形,其边长为质数3.
是三顶点同为蓝色的正三角形,其边长为质数3.
(2)![]() 为红点,考虑点
为红点,考虑点![]() ,若点
,若点![]() 为红点,则
为红点,则![]() 是三顶点同为红色的正三角形,其边长为质数5;若点
是三顶点同为红色的正三角形,其边长为质数5;若点![]() 为蓝点,则
为蓝点,则![]() 是三顶点同为蓝色的正三角形,其边长为质数7.
是三顶点同为蓝色的正三角形,其边长为质数7.
综上,图中总存在三个同色点,两两距离相等且长度为质数3、5、7之一.

【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.