题目内容
【题目】(1)求证:正三角形各顶点到其外接圆上任一切线的距离之和为定值;
(2)猜想空间命题“正四面体各顶点到其外接球的任一切面的距离之和为定值”是否成立?证明你的结论.注:与球只有一个公共点的平面叫做球的切面,这个公共点叫做切点,切点与球心的连线垂直于切面.
【答案】(1)见解析;(2)见解析
【解析】
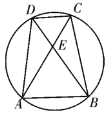
(1)如图,设正![]() 外接圆的圆心为
外接圆的圆心为![]() ,半径为
,半径为![]() ,任意一条切线为
,任意一条切线为![]() ,联结
,联结![]() 交
交![]() 于点
于点![]() .则
.则![]() 为
为![]() 的中点,且
的中点,且![]() .
.
一般地,用记号![]() 表示点
表示点![]() 到切线
到切线![]() 的距离.则
的距离.则![]() ,
,![]() ,
,
得![]() (定值).
(定值).
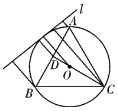
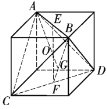
(2)结论是肯定的.证明如下:
如图,作正四面体的外接正方体,在正四面体![]() 中,
中,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 的中心,
的中心,![]() 是正四面体
是正四面体的外接球的球心.则
![]() 、
、![]() 、
、![]() 三点共线,且
三点共线,且![]() 为线段
为线段![]() 的中点(
的中点(![]() 是正方体的中心,
是正方体的中心,![]() 、
、![]() 分别是正方体上、下两面的中心,
分别是正方体上、下两面的中心,![]() 是正方体主对角线的
是正方体主对角线的![]() ).
).
用记号![]() 表示点
表示点![]() 到切面的距离,用
到切面的距离,用![]() 表示外接球的半径长.则
表示外接球的半径长.则
![]() ,
,![]() ,
,![]() ,
,
得![]()
![]() (定值).
(定值).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】黄平县且兰高中全体师生努力下,有效进行了“一对一辅导战略”成绩提高了一倍,下列是“优秀学生”,“中等学生”,“差生”进行“一对一”前后所占比例
战略前 | 战略后 | |||||
优秀学生 | 中等学生 | 差生 | 优秀学生 | 中等学生 | 差生 | |
20% | 50% | 30% | 25% | 45% | 30% | |
则下列结论正确的是( )
A.实行“一对一”辅导战略,差生成绩并没有提高.
B.实行“一对一”辅导战略,中等生成绩反而下降了.
C.实行“一对一”辅导战略,优秀学生成绩提高了.
D.实行“一对一”辅导战略,优秀学生与中等生的成绩没有发生改变.