题目内容

13．如图，在三棱锥ABCD中，点M，N分别是△ABC和△ACD的重心，求证：MN∥BD．

分析 连结AM，AN，并延长分别交BC，CD于F，E，EF为BD的中位线，再根据重心的性质可知，MN∥EF，即可证明结论．

解答 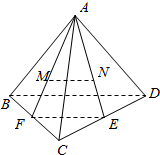解：连结AM，AN，并延长分别交BC，CD于F，E，则F，E分别是BC，CD的中点，连结EF，则EF为BD的中位线，
所以EF平行且等于$\frac{1}{2}$BD，
因为M、N分别是△ABC和△ACD的重心，
所以$\frac{AM}{AF}=\frac{AN}{AE}$=$\frac{2}{3}$，
所以MN∥EF，
所以MN∥BD．

点评 本题主要考查重心和中位线的性质，考查学生的运算能力，要求熟练掌握中位线和重心的比例性质．

练习册系列答案
相关题目
3．已知函数f（x）=x2-ax，（a＞0），$g（x）=sinxsin（{x+\frac{π}{6}}）-\frac{{\sqrt{3}}}{4}$，命题p：an=f（n）是递增数列，命题q：g（x）在（a，π）上有且仅有2条对称轴．
①求g（x）的周期和单调递增区间；
②若p∧q为真，求a的取值范围．
4．已知各顶点都在同一个球面上的正四棱锥高为3，底面边长为$\sqrt{6}$，则这个球的表面积是16π．
1．设函数f（x）在x=0处可导，且f（0）=0，函数g（x）=$\left\{\begin{array}{l}{\frac{f（x）}{x}，x≠0}\\{a，x=0}\end{array}\right.$，试确定a的值，使g（x）在x=0处连续．
8．若直线y=kx-1与双曲线x2-y2=1的左支有两个公共点，则k的取值范围是（　　）
A．（-$\sqrt{2}$，0）B．（-$\sqrt{2}$，$\sqrt{2}$）C．（-$\sqrt{2}$，-1）D．（-$\sqrt{2}$，-1]
18．已知tanα＜0，cosα＜0．
（1）求角α的集合；
（2）求角$\frac{α}{2}$的终边所在的象限；
（3）试判断sin$\frac{α}{2}$cos$\frac{α}{2}$，tan$\frac{α}{2}$的符号．
5．已知函数y=-x2+mx-2，x∈[0，5]，在x=2处取得最大值．
（1）求m的值，并写出函数的单调区间；
（2）求函数的最大值、最小值．
2．如果棱长为2$\sqrt{2}$的正四面体的顶点都在一个球面上，那么这个球的表面积是（　　）
A．8πB．12πC．16πD．20π
3．直线3x+4y+12=0与⊙C：（x-1）2+（y-1）2=9的位置关系是（　　）
A．相交并且过圆心B．相交不过圆心C．相切D．相离

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网