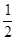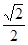题目内容
(本小题满分12分)
已知单调递增的等比数列{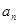 }满足:
}满足: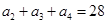 ,且
,且 是
是 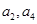 的等差中
的等差中
项.(1)求数列{an}的通项公式.
(2)若 =
=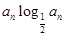 ,sn为数列
,sn为数列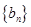 的前
的前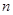 项和,求证:sn
项和,求证:sn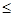
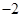 .
.
已知单调递增的等比数列{
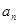 }满足:
}满足: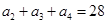 ,且
,且 是
是 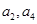 的等差中
的等差中项.(1)求数列{an}的通项公式.
(2)若
 =
=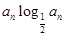 ,sn为数列
,sn为数列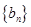 的前
的前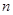 项和,求证:sn
项和,求证:sn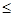
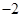 .
.解:(1)设等比数列
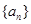 的首项为
的首项为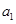 ,公比为q,
,公比为q,依题意,有
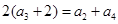 代入a2+a3+a4=28,得
代入a2+a3+a4=28,得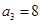 ┉┉ 2分
┉┉ 2分∴
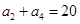 ∴
∴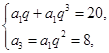 解之得
解之得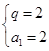 或
或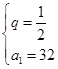 ┉┉┉4分
┉┉┉4分又
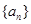 单调递增,∴
单调递增,∴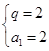 ∴
∴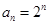 . ┉┉┉┉┉6分
. ┉┉┉┉┉6分(2)
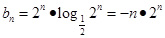 , ┉┉┉┉┉7分
, ┉┉┉┉┉7分∴
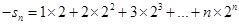 ①
①∴
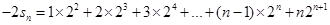 ②
②∴①-②得

=
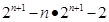 ┉┉┉10分
┉┉┉10分 =
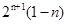
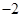 ,
,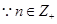 ,
, 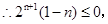
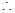 sn
sn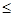
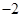 . ┉┉┉12分
. ┉┉┉12分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
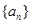 与
与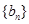 满足:
满足: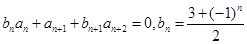 ,
,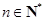 ,且
,且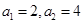 .
.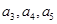 的值;
的值;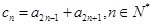 ,证明:
,证明: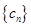 是等比数列
是等比数列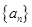 的前
的前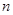 项和为
项和为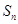 ,满足
,满足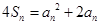 ,
,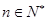 .(Ⅰ)求数列
.(Ⅰ)求数列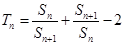 ,证明:
,证明: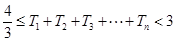
 是首项为
是首项为 ,公比
,公比 的等比数列,设
的等比数列,设 ,数列
,数列 .
.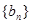 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和Sn.
的前n项和Sn.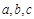 成等比数列,命题q:
成等比数列,命题q: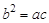 ,那么p是q的( )条件
,那么p是q的( )条件 a7= .
a7= . 中,a1=3,前三项和为21,则a3 + a4 + a5 = ( )
中,a1=3,前三项和为21,则a3 + a4 + a5 = ( )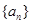 的公比为正数,且
的公比为正数,且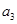 ·
·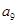 =2
=2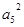 ,
,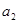 =1,则
=1,则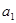 = ( )
= ( )