题目内容
4.一条斜率为2的直线与抛物线y2=4x相交于A、B两点,已知$|{AB}|=3\sqrt{5}$.求该直线方程.分析 设直线方程为y=2x+b,联立方程,可得y2-2y+2b=0,由韦达定理得:y1+y2=2,y1•y2=2b,代入弦长公式,求出b值,可得答案.
解答 解:设直线方程为y=2x+b,即2x=y-b,
代入抛物线y2=4x可得:y2=2(y-b),即y2-2y+2b=0,
由韦达定理得:y1+y2=2,y1•y2=2b,
则|AB|=$\sqrt{1+(\frac{1}{2})^{2}}$$\sqrt{{(y}_{1}+{y}_{2})^{2}-4{y}_{1}•{y}_{2}}$=$\frac{\sqrt{5}}{2}$$\sqrt{4-8b}$=3$\sqrt{5}$.
解得:b=-4,
故直线方程为:y=2x-b,即2x-y-8=0
点评 本题考查的知识点是抛物线的简单性质,弦长公式,是直线与圆锥曲线的简单综合,难度中档.

练习册系列答案
相关题目
9.已知$f(x)=\left\{{\begin{array}{l}{{2^{x-2}}}\\{a-x}\end{array}}\right.$ $\begin{array}{l}{x>1}\\{0≤x<1}\end{array}$,且$f({\frac{f(2)}{2}})=\frac{1}{2}$,则实数a=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
14.函数 y=cos2x+2cosx的值域是( )
| A. | [-1,3] | B. | $[-\frac{3}{2},3]$ | C. | $[-\frac{3}{2},-1]$ | D. | $[\frac{3}{2},3]$ |
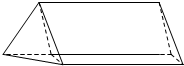 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.