题目内容
定义在 上的偶函数
上的偶函数 满足
满足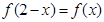 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )
 上的偶函数
上的偶函数 满足
满足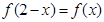 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )A.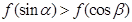 | B.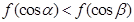 |
C. | D.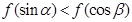 |
D
试题分析:由
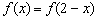 可知
可知 图象关于
图象关于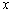
 对称,又因为
对称,又因为 为偶函数图象关于
为偶函数图象关于 对称,可得到
对称,可得到 为周期函数且最小正周期为2,结合
为周期函数且最小正周期为2,结合 在区间
在区间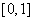 上是减函数,画出满足题意的一个函数图象如右
上是减函数,画出满足题意的一个函数图象如右 图所示.因为
图所示.因为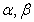 是钝角三角形的两个锐角,所以
是钝角三角形的两个锐角,所以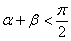 ,
,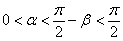 ,所以
,所以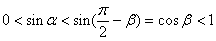 ,
,所以
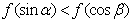 .
.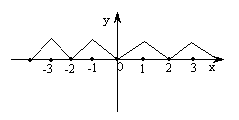 ,故选D.
,故选D.点评:本题主要考查了函数的奇偶性、单调性等综合应用,解决的关键一是由f(2-x)=f(x),偶函数满足的f(-x)=f(x)可得函数的周期,关键二是要熟练掌握偶函数对称区间上的单调性相反的性质,关键三是要α,β是钝角三角形的两个锐角可得0°<α+β<90°即0°<α<90°-β.本题是综合性较好的试题

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 小时,写出
小时,写出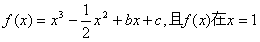 处取得极值.
处取得极值.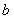 的值;
的值;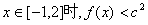 恒成立,求
恒成立,求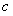 的取值范围;
的取值范围;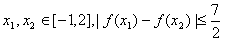 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.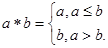 如
如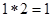 ,则函数
,则函数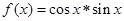 的值域为( )
的值域为( )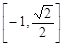
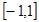

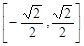
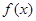 =
=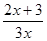 ,数列
,数列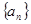 满足
满足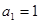 ,
,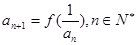 。(12分)
。(12分)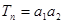 -
-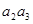 +
+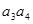 -
-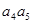 +…+
+…+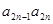 -
-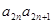 求
求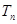 ;
;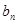 =
=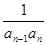 (
(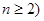 ,
,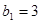 ,
,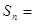
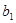 +
+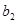 +
+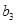 +┅
+┅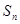 <
<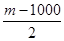 对一切
对一切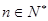 都成立,求最小的正整数
都成立,求最小的正整数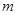 。
。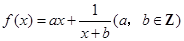 ,曲线
,曲线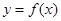 在点
在点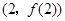 处的切线方程
处的切线方程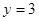 .
.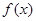 的解析式,并判断函数
的解析式,并判断函数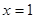 和直线
和直线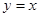 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.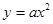 (
(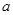 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由) (万元)和
(万元)和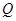 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?