题目内容
(本小题满分14分)
已知函数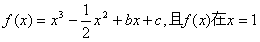 处取得极值.
处取得极值.
(Ⅰ)求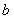 的值;
的值;
(Ⅱ)若当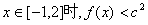 恒成立,求
恒成立,求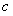 的取值范围;
的取值范围;
(Ⅲ)对任意的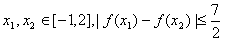 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
已知函数
 处取得极值.
处取得极值.(Ⅰ)求
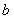 的值;
的值;(Ⅱ)若当
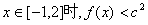 恒成立,求
恒成立,求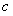 的取值范围;
的取值范围;(Ⅲ)对任意的
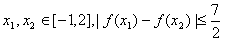 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.(1) b=-2(2) c<-1或c>2.(3)运用函数的单调性,结合最大值与最小值差的绝对值满足不等式即可。
试题分析:解:(Ⅰ)∵f(x)=x3-
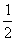 x2+bx+c,∴f′(x)=3x2-x+b. ……2分
x2+bx+c,∴f′(x)=3x2-x+b. ……2分∵f(x)在x=1处取得极值,∴f′(1)=3-1+b=0
∴b=-2. ……3分
经检验,符合题意. ……4分
(Ⅱ)f(x)=x3-
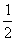 x2-2x+c.∵f′(x)=3x2-x-2=(3x+2)(x-1), …5分
x2-2x+c.∵f′(x)=3x2-x-2=(3x+2)(x-1), …5分| x | 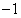 | 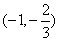 | 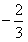 | 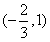 | 1 | (1,2) | 2 |
| f′(x) | | + | 0 | - | 0 | + | |
| f(x) | 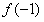 |  | 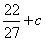 |  | 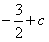 |  | 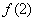 |
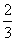 时,f(x)有极大值
时,f(x)有极大值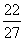 +c.
+c.又
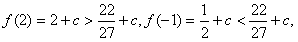
∴x∈[-1,2]时,f(x)最大值为f(2)=2+c. ……8分
∴c2>2+c. ∴c<-1或c>2. …………10分(Ⅲ)对任意的
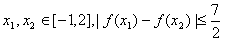 恒成立.
恒成立.由(Ⅱ)可知,当x=1时,f(x)有极小值
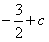 .又
.又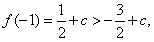 …12分∴x∈[-1,2]时,f(x)最小值为
…12分∴x∈[-1,2]时,f(x)最小值为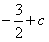 .
.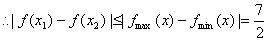 ,故结论成立. ……14分
,故结论成立. ……14分点评:解决该试题的关键是能结合导数的符号判定函数的单调性,让那后结合函数的极值得到最值,属于基础题。

练习册系列答案
相关题目
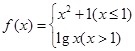 ,则
,则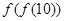 =( )
=( )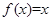 ,
, 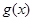 =
=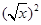
 =
=
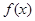 =
=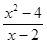 ,
,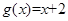
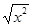
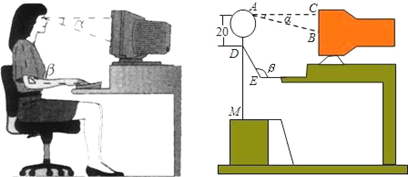
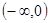 上单调递减的函数是( )
上单调递减的函数是( )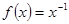
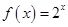
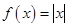
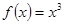
 上的偶函数
上的偶函数 满足
满足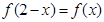 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )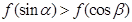
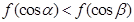

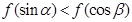
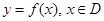 ,若存在常数C,对任意的
,若存在常数C,对任意的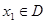 ,存在唯一的
,存在唯一的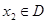 ,使得
,使得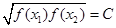 ,则称函数
,则称函数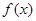 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知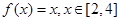 ,则函数
,则函数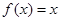 在
在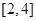 上的几何平均数为( )
上的几何平均数为( ) 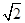 B.
B.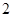 C.
C.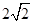 D.
D.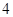
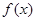 的图象是折线段
的图象是折线段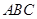 ,其中
,其中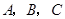 的坐标分别为
的坐标分别为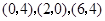 ,则
,则 。
。