题目内容
一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?
每天从报社买进400份时,每月获的利润最大,最大利润为870元
试题分析:
| | 数量(份) | 价格(元) | 金额(元) |
| 买进 | 30x | 0.20 | 6x |
| 卖出 | 20x+10*250 | 0.30 | 6x+750 |
| 退回 | 10(x-250) | 0.08 | 0.8x-200 |
y在x [250,400]上是一次函数.
∴x=400份时,y取得最大值870元.
答:每天从报社买进400份时,每月获的利润最大,最大利润为870元.
点评:解决的关键是对于利润函数的表示和函数性质的运用,属于基础题。

练习册系列答案
相关题目
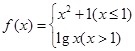 ,则
,则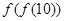 =( )
=( ) +b2(a1,a2,b2∈R).
+b2(a1,a2,b2∈R).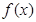 和
和 的图象关于原点对称,且
的图象关于原点对称,且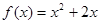 .
. 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数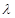 的取值范围
的取值范围 ,其中
,其中 ,
, ,则在同一直角坐标系中所确定的不同点的个数是( )
,则在同一直角坐标系中所确定的不同点的个数是( ) 是(-
是(- 上的减函数,
上的减函数, 的取值范围是( )
的取值范围是( )



 的定义域为
的定义域为 ,其中a、b为任
,其中a、b为任 时,研究
时,研究 其中k是正整数,对一切正整数k不等式
其中k是正整数,对一切正整数k不等式 都有解,求m的取值范围。
都有解,求m的取值范围。 上的偶函数
上的偶函数 满足
满足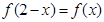 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则下列结论正确的是( )
是钝角三角形的两个锐角,则下列结论正确的是( )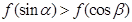
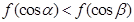

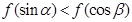
 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数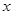 都有
都有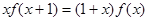 ,则
,则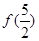 的值是( )
的值是( )


