题目内容
(14分)已知定义在正实数集上的函数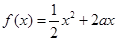 ,
,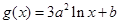 ,其中
,其中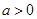 .设两曲线
.设两曲线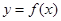 ,
,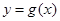 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用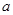 表示
表示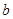 ,并求
,并求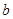 的最大值;
的最大值;
(2)判断当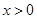 时,
时,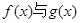 的大小,并证明.
的大小,并证明.
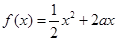 ,
,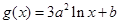 ,其中
,其中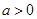 .设两曲线
.设两曲线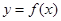 ,
,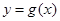 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.(1)用
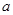 表示
表示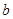 ,并求
,并求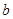 的最大值;
的最大值;(2)判断当
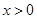 时,
时,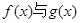 的大小,并证明.
的大小,并证明.(1)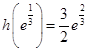 .
.
(2)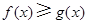 .证明见解析。
.证明见解析。
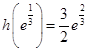 .
.(2)
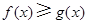 .证明见解析。
.证明见解析。(I)设公共点为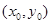 ,然后利用导数求出此点处的切线,根据切线重合.解出切点的横坐标,从而可找到b关于a的表达式.然后再利用导数研究其最值即可.
,然后利用导数求出此点处的切线,根据切线重合.解出切点的横坐标,从而可找到b关于a的表达式.然后再利用导数研究其最值即可.
(2)本小题可构造函数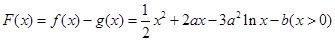 ,然后利用导数研究其最值,从而比较出f(x)与g(x)的大小关系.
,然后利用导数研究其最值,从而比较出f(x)与g(x)的大小关系.
(1)设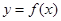 与
与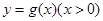 在公共点
在公共点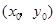 处的切线相同.
处的切线相同.
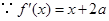 ,
,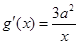 ,由题意
,由题意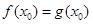 ,
,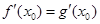 .
.
即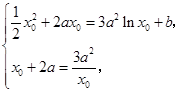 由
由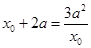 得:
得: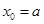 ,或
,或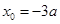 (舍去).
(舍去).
即有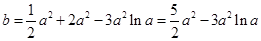 .
.
令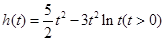 ,则
,则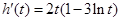 .于是
.于是
当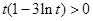 ,即
,即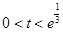 时,
时,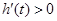 ;当
;当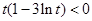 ,即
,即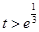 时,
时,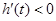 .
.
故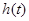 在
在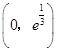 为增函数,在
为增函数,在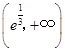 为减函数,
为减函数,
于是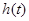 在
在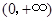 的最大值为
的最大值为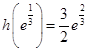 .
.
(2)设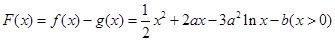 ,
,
则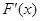
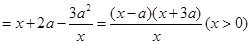 .
.
故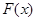 在
在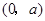 为减函数,在
为减函数,在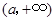 为增函数,
为增函数,
于是函数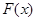 在
在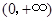 上的最小值是
上的最小值是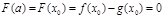 .
.
故当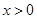 时,有
时,有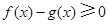 ,即当
,即当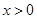 时,
时,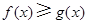 .
.
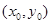 ,然后利用导数求出此点处的切线,根据切线重合.解出切点的横坐标,从而可找到b关于a的表达式.然后再利用导数研究其最值即可.
,然后利用导数求出此点处的切线,根据切线重合.解出切点的横坐标,从而可找到b关于a的表达式.然后再利用导数研究其最值即可.(2)本小题可构造函数
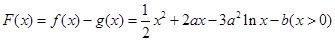 ,然后利用导数研究其最值,从而比较出f(x)与g(x)的大小关系.
,然后利用导数研究其最值,从而比较出f(x)与g(x)的大小关系.(1)设
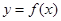 与
与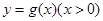 在公共点
在公共点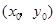 处的切线相同.
处的切线相同.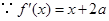 ,
,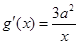 ,由题意
,由题意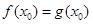 ,
,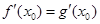 .
.即
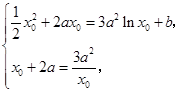 由
由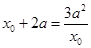 得:
得: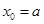 ,或
,或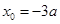 (舍去).
(舍去).即有
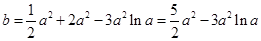 .
.令
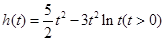 ,则
,则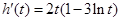 .于是
.于是当
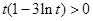 ,即
,即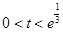 时,
时,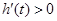 ;当
;当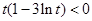 ,即
,即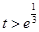 时,
时,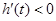 .
.故
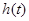 在
在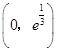 为增函数,在
为增函数,在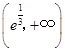 为减函数,
为减函数,于是
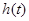 在
在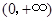 的最大值为
的最大值为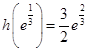 .
.(2)设
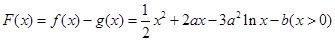 ,
,则
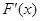
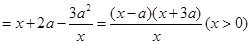 .
.故
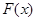 在
在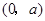 为减函数,在
为减函数,在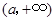 为增函数,
为增函数,于是函数
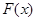 在
在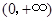 上的最小值是
上的最小值是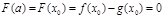 .
.故当
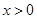 时,有
时,有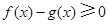 ,即当
,即当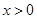 时,
时,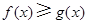 .
.
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 ,若
,若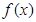 的单调减区间是 (0,4),则在曲线
的单调减区间是 (0,4),则在曲线 的切线中,斜率最小的切线方程是_________________.
的切线中,斜率最小的切线方程是_________________.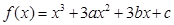 在
在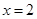 处有极值,其图象在
处有极值,其图象在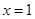 处的切线与直线
处的切线与直线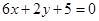 平行.
平行.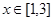 时,
时,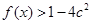 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?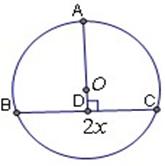
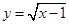 相切的切线方程为 ( )
相切的切线方程为 ( )
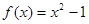 与函数
与函数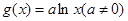 .
.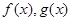 的图象在点
的图象在点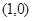 处有公共的切线,求实数
处有公共的切线,求实数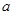 的值;
的值;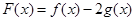 ,求函数
,求函数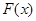 的极值.
的极值.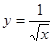 在点
在点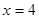 处的导数是
处的导数是 
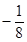
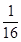 (
(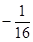

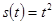 运动,则t=2时的瞬时速度为( )
运动,则t=2时的瞬时速度为( )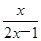 在点(1,1)处的切线方程为
在点(1,1)处的切线方程为