题目内容
(本题满分10分)在半径为 的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?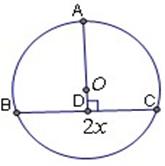
 的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
的圆内,作内接等腰三角形,当底边上高为多少时,它的面积最大?
当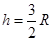 时,等腰三角形的面积最大.
时,等腰三角形的面积最大.
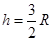 时,等腰三角形的面积最大.
时,等腰三角形的面积最大.本试题主要考查了导数解决实际问题的中的最值问题的运用。
利用已知条件设出变量,然后表示半径为R的圆内,作内接等腰三角形的面积,结合导数的思想得到极值,进而得到最值。
如图,设圆内接等腰三角形的底边长为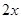 ,高为
,高为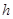 ,
,
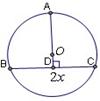
那么
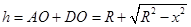 ,
,
解得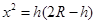 ,于是内接三角形的面积为:
,于是内接三角形的面积为:
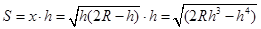 ,
,
从而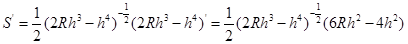
 ,
,
令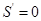 ,解得
,解得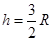 ,由于不考虑不存在的情况,所在区间
,由于不考虑不存在的情况,所在区间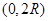 上列表示如下:
上列表示如下:
由此表可知,当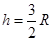 时,等腰三角形的面积最大.
时,等腰三角形的面积最大.
利用已知条件设出变量,然后表示半径为R的圆内,作内接等腰三角形的面积,结合导数的思想得到极值,进而得到最值。
如图,设圆内接等腰三角形的底边长为
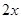 ,高为
,高为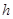 ,
,
那么
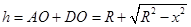 ,
,解得
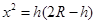 ,于是内接三角形的面积为:
,于是内接三角形的面积为: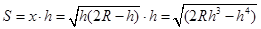 ,
,从而
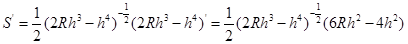
 ,
,令
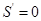 ,解得
,解得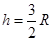 ,由于不考虑不存在的情况,所在区间
,由于不考虑不存在的情况,所在区间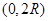 上列表示如下:
上列表示如下: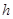 | 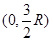 | 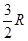 | 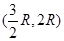 |
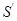 |  |  | 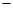 |
 | 增函数 | 最大值 | 减函数 |
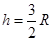 时,等腰三角形的面积最大.
时,等腰三角形的面积最大.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
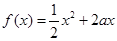 ,
,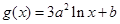 ,其中
,其中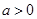 .设两曲线
.设两曲线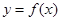 ,
,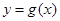 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.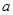 表示
表示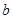 ,并求
,并求 时,
时,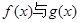 的大小,并证明.
的大小,并证明.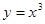 在点
在点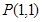 的切线方程为 .
的切线方程为 .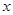 个月,顾客对某种商品的需求总量
个月,顾客对某种商品的需求总量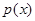 (单位:件)与
(单位:件)与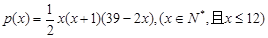 .该商品第
.该商品第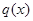 (单位:元)与x的近似关系是:
(单位:元)与x的近似关系是: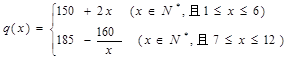
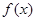 件与
件与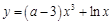 存在垂直于
存在垂直于 轴的切线,函数
轴的切线,函数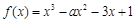 在
在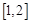 上单调递增,则
上单调递增,则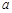 的范围为 .
的范围为 . 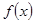 的定义域为
的定义域为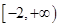 ,部分对应值如下表,
,部分对应值如下表,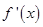 为
为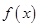 的导函数,函数
的导函数,函数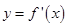 的图象如图所示.若实数
的图象如图所示.若实数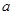 满足
满足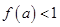 ,则
,则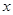
 2
2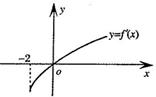
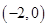 B.
B.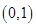 C.
C.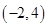 D.
D.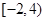
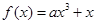 在定义域
在定义域 上恰有三个单调区间,则
上恰有三个单调区间,则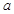 的取值范围是( )
的取值范围是( )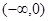
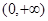
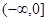
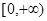
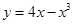 在点
在点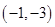 处的切线方程是____________
处的切线方程是____________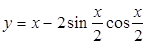 ,则
,则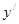 =
=