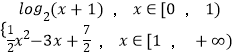题目内容
【题目】已知命题p： 
，命题q：x∈R，x2﹣2ax+2﹣a=0，若命题“p∧q”是真命题，则实数a的取值范围是（ ）
A.（﹣∞，﹣2]∪{1}
B.（﹣∞，﹣2]∪[1，2]
C.[1，+∞）
D.[﹣2，1]
【答案】A
【解析】解：命题p： 
，∴a≤[（x﹣1）2+1]min=1．
命题q：x∈R，x2﹣2ax+2﹣a=0，∴△=4a2﹣4（2﹣a）≥0，解得a≥1或a≤﹣2．
∵命题“p∧q”是真命题，∴p与q都是真命题．
∴ 
，解得a=1或a≤﹣2．
则实数a的取值范围是（﹣∞，﹣2]∪{1}．
故选：A．
【考点精析】认真审题，首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真)．
练习册系列答案
相关题目
