题目内容
【题目】已知a∈R，函数f（x）=x2（x﹣a）．
（1）若函数f（x）在区间 
内是减函数，求实数a的取值范围；
（2）求函数f（x）在区间[1，2]上的最小值h（a）．
【答案】
（1）解：∵f（x）=x3﹣ax2，
∴f'（x）=3x2﹣2ax．
∵函数f（x）在区间 
内是减函数，
∴f'（x）=3x2﹣2ax≤0在 上恒成立．
即 
在 上恒成立，
∵ 
，
∴a≥1．故实数a的取值范围为[1，+∞）
（2）解：∵ 
，
令f'（x）=0得 
．
①若a≤0，则当1≤x≤2时，f'（x）＞0，
所以f（x）在区间[1，2]上是增函数，
所以h（a）=f（1）=1﹣a．
②若 
，即 
，
则当1≤x≤2时，f'（x）＞0，
所以f（x）在区间[1，2]上是增函数，
所以h（a）=f（1）=1﹣a
③若 
，即 
，
则当 
时，f'（x）＜0；
当 
时，f'（x）＞0．
∴f（x）在 
上是减函数，在 
上是增函数．
∴ 
．
④若a≥3，即 
，
则当1＜x＜2时，f'（x）＜0，
所以f（x）在区间[1，2]上是减函数．
所以h（a）=f（2）=8﹣4a．
综上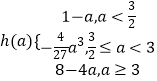 
【解析】（1）由f（x）=x3﹣ax2 ， 知f'（x）=3x2﹣2ax．由函数f（x）在区间 内是减函数，知f'（x）=3x2﹣2ax≤0在 上恒成立．由此能求出实数a的取值范围．（2）由 ，令f'（x）=0得 ．若a≤0，则当1≤x≤2时，f'（x）＞0，所以h（a）=f（1）=1﹣a；若 ，当1≤x≤2时，f'（x）＞0，所以h（a=f（1）=1﹣a；若 ， 时，f'（x）＜0；当 时，f'（x）＞0．所以 若a≥3，当1＜x＜2时，f'（x）＜0，所以h（a）=f（2）=8﹣4a．由此能得到结果．
【考点精析】掌握函数的最大(小)值与导数是解答本题的根本，需要知道求函数
在
上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．
