题目内容
(本小题满分14分)
如图,在等腰直角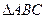 中,
中,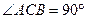 ,
,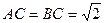 ,
,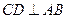 ,
,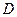 为垂足.沿
为垂足.沿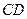 将
将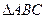 对折,连结
对折,连结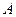 、
、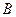 ,使得
,使得 .
.
(1)对折后,在线段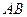 上是否存在点
上是否存在点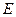 ,使
,使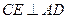 ?若存在,求出
?若存在,求出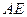 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(2)对折后,求二面角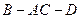 的平面角的正切值.
的平面角的正切值.
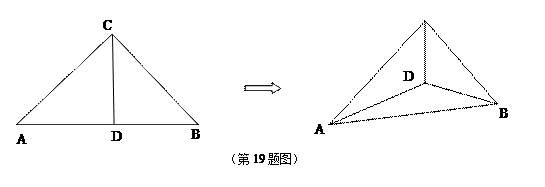
如图,在等腰直角
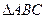 中,
中,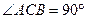 ,
,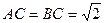 ,
,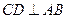 ,
,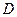 为垂足.沿
为垂足.沿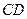 将
将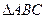 对折,连结
对折,连结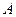 、
、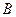 ,使得
,使得 .
.(1)对折后,在线段
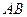 上是否存在点
上是否存在点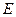 ,使
,使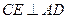 ?若存在,求出
?若存在,求出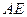 的长;若不存在,说明理由;
的长;若不存在,说明理由; (2)对折后,求二面角
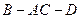 的平面角的正切值.
的平面角的正切值.
|

(1)过
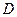 作
作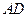 的垂线,与
的垂线,与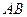 的交于点
的交于点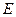 ,点
,点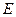 就是
就是 满足条件的唯一点

(2)
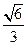

解:(1)在线段
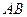 上存在点
上存在点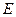 ,使
,使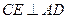 .
.  ……………………………1分
……………………………1分由等腰直角
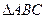 可知,对折后,
可知,对折后,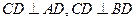 ,
, .
.在
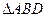 中,
中,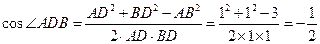 ,
,∴
 ,
,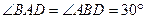 . ……………………………4分
. ……………………………4分过
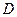 作
作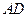 的垂线,与
的垂线,与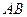 的交于点
的交于点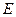 ,点
,点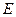 就是
就是 满足条件的唯一点.理由如下:
连结
 ,
,∵
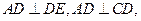
 ,
,∴
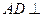 平面
平面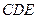 ,
,∴
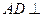
 ,
,即在线段
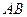 上存在点
上存在点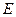 ,使
,使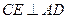 . ……………………………6分
. ……………………………6分在
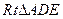 中,
中,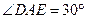 ,
,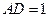 ,得
,得 .……………7分
.……………7分(2)
 对折后,作
对折后,作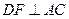 于
于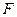 ,连结
,连结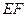 ,
,∵
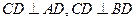 ,
,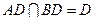 ,
,∴
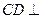 平面
平面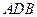 ,
,∴平面
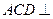 平面
平面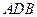 . ……………………………9分
. ……………………………9分∵
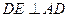 ,且平面
,且平面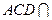 平面
平面 ,
,∴
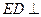 平面
平面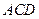 .
.而
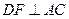 ,所以
,所以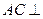 平面
平面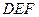 ,
,即
 为二面角
为二面角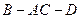 的平面角. ……11分
的平面角. ……11分在
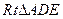 中,
中,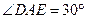 ,
,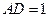 ,
,在
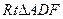 中,
中, ,
,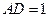 ,得
,得 . ……………………………12分
. ……………………………12分在
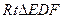 中,
中,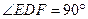 ,
,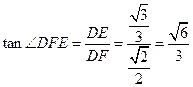 ,
, 即二面角
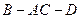 的平面角的正切值等于
的平面角的正切值等于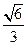 . ……………………………14分
. ……………………………14分
练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
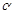 外一点,和平面
外一点,和平面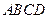 为矩形,
为矩形,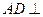
 平面ABE
平面ABE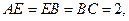
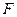 为
为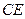 上的点,且
上的点,且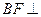 平
平 面
面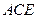 ,
,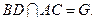
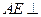 平面
平面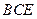 ;
;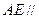 平面
平面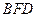 ;
;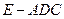 的体积.
的体积.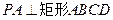 所在的平面,
所在的平面,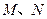 分别为
分别为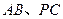 的中点,
的中点,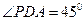 ,
,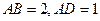
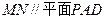 ;
; 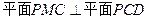 ;
;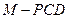 的体积.
的体积.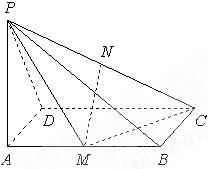
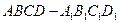 中,
中,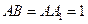 ,
,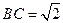 ,
,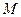 是
是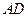 中点,
中点,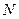 是
是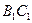 中点.
中点.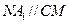 ;
; ⊥平面
⊥平面 .
.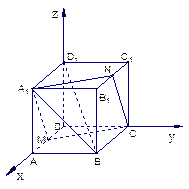
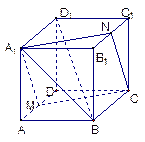
 中,
中, 是棱
是棱 的中点,
的中点, 为平面
为平面 内一点,
内一点,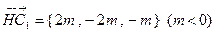 .
.
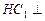 平面
平面 与平面
与平面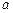 ,求三棱锥
,求三棱锥 的体积.
的体积. 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。 
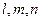 是三条不重合的直线,
是三条不重合的直线,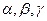 是三个不重合的平面,给出下列四个命题:
是三个不重合的平面,给出下列四个命题: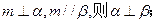
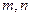 与平面
与平面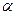 所成的角相等,则
所成的角相等,则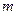 //
//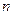 ;
;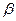 ,
,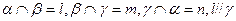 ,则
,则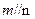 ;
;