题目内容
(本小题满分5分)直线a,b相交于O,且a,b成角600, 过O与a,b都成600角的直线有( )
| A.1条 | B.2条 | C.3条 | D.4条 |
C
考点:
分析:根据等角定理可知将经过空间任意一点O/,作直线a/、b/,并使a/∥a、b/∥b,,则a/与b/相交所成的角为600或1200,从而在a/与b/相交所成的平面内,存在1200的角的平分线满足题意,又当射影为600角的平分线时存在两条,得到结论.
解答:解:经过空间任意一点O/,作直线a/、b/,并使a/∥a、b/∥b,,则a/与b/相交所成的角为600或1200,因此,在a/与b/相交所成的平面内,存在1200的角的平分线满足题意,又当射影为600角的平分线时存在两条,故过点O/与a、b都成600角的直线有3条
故答案为:C
点评:空间问题平面化是研究立体几何的常用方法,要注意想象能力的培养,属于基础题.
分析:根据等角定理可知将经过空间任意一点O/,作直线a/、b/,并使a/∥a、b/∥b,,则a/与b/相交所成的角为600或1200,从而在a/与b/相交所成的平面内,存在1200的角的平分线满足题意,又当射影为600角的平分线时存在两条,得到结论.
解答:解:经过空间任意一点O/,作直线a/、b/,并使a/∥a、b/∥b,,则a/与b/相交所成的角为600或1200,因此,在a/与b/相交所成的平面内,存在1200的角的平分线满足题意,又当射影为600角的平分线时存在两条,故过点O/与a、b都成600角的直线有3条
故答案为:C
点评:空间问题平面化是研究立体几何的常用方法,要注意想象能力的培养,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
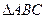 中,
中,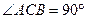 ,
,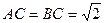 ,
,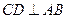 ,
,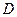 为垂足.沿
为垂足.沿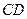 将
将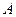 、
、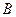 ,使得
,使得 .
.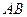 上是否存在点
上是否存在点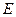 ,使
,使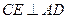 ?若存在,求出
?若存在,求出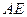 的长;若不存在,说明理由;
的长;若不存在,说明理由; 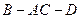 的平面角的正切值.
的平面角的正切值.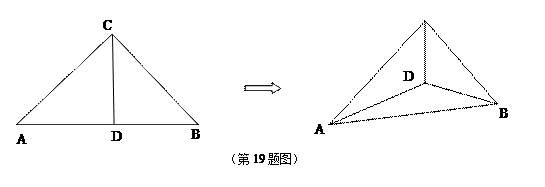
 棱锥
棱锥 的底面
的底面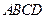 是
是 正方形,侧棱
正方形,侧棱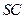 的中点
的中点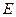 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形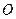 ,
, 顶点
顶点 在截面
在截面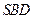 内
内 的射影恰好是
的射影恰好是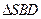 的重心
的重心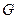 .
.
 与底面
与底面 ,求此四棱锥过点
,求此四棱锥过点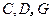 的截面面积.
的截面面积.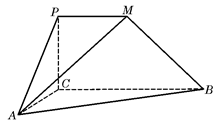
 中,
中,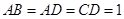 ,
, 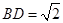 ,
,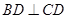 .将四边形
.将四边形 折成四面体
折成四面体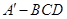 ,使平面
,使平面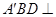 平面
平面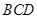 ,则下列结论正确的是
,则下列结论正确的是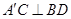
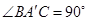
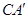 与平面
与平面 所成的角为
所成的角为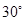
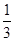
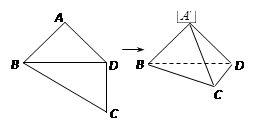
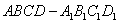 中,
中,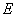 、
、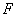 分别是棱
分别是棱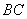 ,
,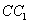 上的点,
上的点,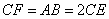 ,
,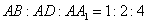 .
.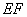 与
与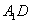 所成角的余弦值;
所成角的余弦值;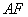
 平面
平面
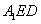 ;
;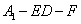 的正弦值.
的正弦值.

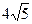 (1)设M是PC上的一点,证明:平面MBD⊥平面PAD(2)求四棱锥P-ABCD的体积
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD(2)求四棱锥P-ABCD的体积