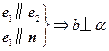题目内容
如图,在四棱 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。

⑴求证:CD⊥PD;
⑵求证:EF∥平面PAD;
⑶若直线EF⊥平面PCD,求平面PCD与平面ABCD所成二面角的大小
 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。 
⑴求证:CD⊥PD;
⑵求证:EF∥平面PAD;
⑶若直线EF⊥平面PCD,求平面PCD与平面ABCD所成二面角的大小
(1)证明略
(2)证明略
(3)45°
略

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 ,∠PAB=60°。
,∠PAB=60°。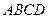 中,
中,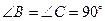 ,
,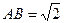 ,
,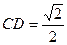 ,
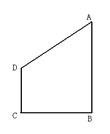
,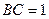 .将
.将 )绕
)绕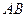 所在的直线旋转一周,形成一个几何体.
所在的直线旋转一周,形成一个几何体.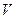 ;
;
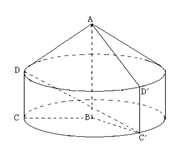 (2)设直角梯形
(2)设直角梯形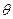 (
(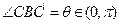 )至
)至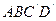 ,问:是否存在
,问:是否存在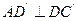 .若存在,求角
.若存在,求角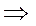
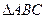 中,
中,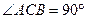 ,
,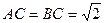 ,
,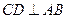 ,
,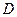 为垂足.沿
为垂足.沿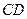 将
将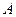 、
、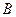 ,使得
,使得 .
.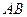 上是否存在点
上是否存在点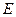 ,使
,使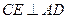 ?若存在,求出
?若存在,求出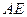 的长;若不存在,说明理由;
的长;若不存在,说明理由; 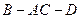 的平面角的正切值.
的平面角的正切值.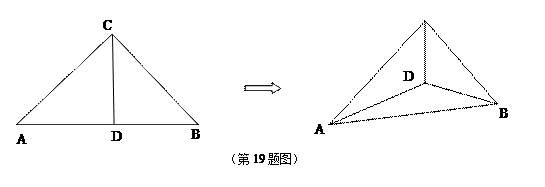
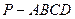 中,底面
中,底面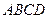 是直角梯形,
是直角梯形,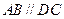 ,
,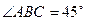 ,
,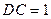 ,
,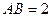 ,
,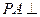 平面
平面 .
. 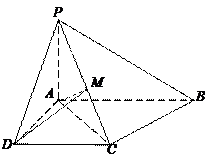
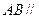 平面
平面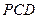 ;
;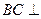 平面
平面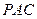 ;
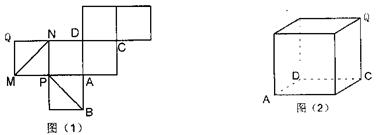
;
 棱锥
棱锥 的底面
的底面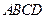 是
是 正方形,侧棱
正方形,侧棱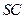 的中点
的中点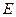 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形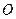 ,
, 顶点
顶点 在截面
在截面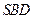 内
内 的射影恰好是
的射影恰好是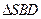 的重心
的重心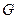 .
.
 与底面
与底面 ,求此四棱锥过点
,求此四棱锥过点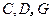 的截面面积.
的截面面积.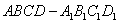 中,
中,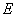 、
、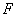 分别是棱
分别是棱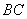 ,
,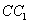 上的点,
上的点,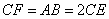 ,
,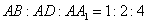 .
.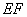 与
与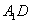 所成角的余弦值;
所成角的余弦值;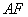
 平面
平面
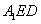 ;
;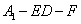 的正弦值.
的正弦值.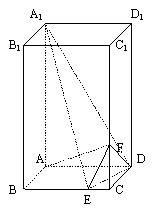
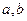 的方向向量是
的方向向量是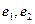 ,平面
,平面 的法向量是
的法向量是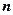 ,则下列推理中
,则下列推理中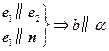 ②
②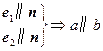
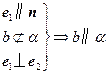 ④
④