题目内容
如图,正方体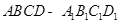 的棱长为
的棱长为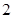 ,
,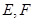 分别为棱
分别为棱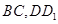 上的点,给出下列命题:
上的点,给出下列命题:
①在平面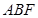 内总存在与直线
内总存在与直线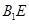 平行的直线;
平行的直线;
②若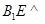 平面
平面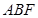 ,则
,则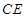 与
与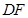 的长度之和为
的长度之和为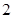 ;
;
③存在点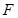 使二面角
使二面角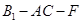 的大小为
的大小为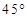 ;
;
④记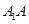 与平面
与平面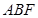 所成的角为
所成的角为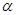 ,
,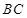 与平面
与平面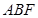 所成的角为
所成的角为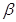 ,则
,则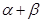 的大小与点
的大小与点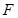 的位置无关.
的位置无关.
其中真命题的序号是 ▲ . (写出所有真命题的序号)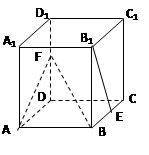
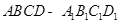 的棱长为
的棱长为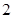 ,
,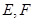 分别为棱
分别为棱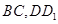 上的点,给出下列命题:
上的点,给出下列命题:①在平面
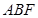 内总存在与直线
内总存在与直线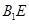 平行的直线;
平行的直线;②若
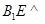 平面
平面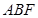 ,则
,则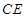 与
与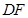 的长度之和为
的长度之和为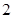 ;
;③存在点
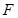 使二面角
使二面角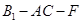 的大小为
的大小为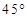 ;
;④记
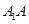 与平面
与平面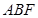 所成的角为
所成的角为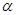 ,
,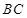 与平面
与平面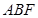 所成的角为
所成的角为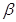 ,则
,则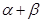 的大小与点
的大小与点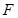 的位置无关.
的位置无关.其中真命题的序号是 ▲ . (写出所有真命题的序号)
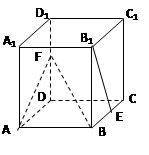
②④.
当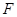 与
与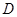 重合,
重合,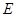 与
与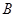 重合时,可得
重合时,可得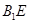 即
即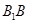 垂直于面
垂直于面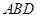 即
即 ,命题①不正确;
,命题①不正确;
在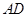 上取一点
上取一点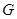 使得
使得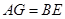 ,连接
,连接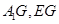 ,可得四边形
,可得四边形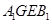 为平行四边形,所以
为平行四边形,所以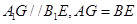 。因为
。因为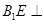 面
面 ,所以
,所以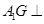 面
面 ,则
,则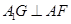 ,从而可得
,从而可得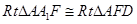 ,所以
,所以 。从而有
。从而有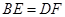 ,所以
,所以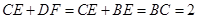 ,命题②正确;
,命题②正确;
连接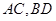 ,设交点为
,设交点为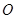 ,连接
,连接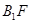 。由对称可得
。由对称可得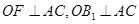 ,所以
,所以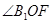 是二面角
是二面角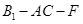 的平面角。设
的平面角。设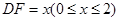 ,则
,则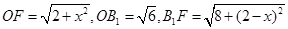 。由余弦定理可得,
。由余弦定理可得,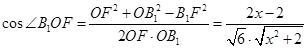 。记
。记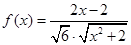 ,则
,则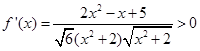 ,则
,则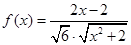 在区间
在区间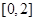 上单调递增,所以
上单调递增,所以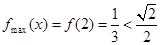 ,所以不存在点
,所以不存在点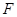 使得二面角
使得二面角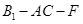 的大小为
的大小为 ,命题③不正确;
,命题③不正确;
因为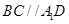 ,所以
,所以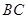 与平面
与平面 所成角等于
所成角等于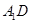 与平面
与平面 所成角。过点
所成角。过点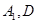 分别作
分别作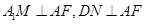 。因为
。因为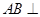 面
面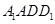 ,所以
,所以 ,从而有
,从而有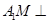 面
面 ,
,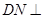 面
面 ,则
,则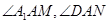 分别是
分别是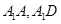 与平面
与平面 所成角,从而有
所成角,从而有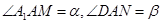 ,所以
,所以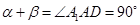 恒为定值,,命题④正确。
恒为定值,,命题④正确。
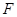 与
与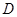 重合,
重合,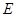 与
与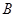 重合时,可得
重合时,可得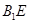 即
即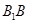 垂直于面
垂直于面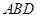 即
即 ,命题①不正确;
,命题①不正确;在
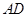 上取一点
上取一点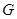 使得
使得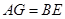 ,连接
,连接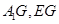 ,可得四边形
,可得四边形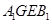 为平行四边形,所以
为平行四边形,所以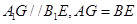 。因为
。因为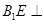 面
面 ,所以
,所以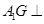 面
面 ,则
,则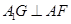 ,从而可得
,从而可得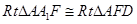 ,所以
,所以 。从而有
。从而有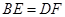 ,所以
,所以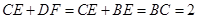 ,命题②正确;
,命题②正确;连接
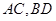 ,设交点为
,设交点为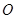 ,连接
,连接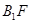 。由对称可得
。由对称可得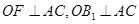 ,所以
,所以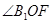 是二面角
是二面角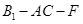 的平面角。设
的平面角。设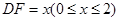 ,则
,则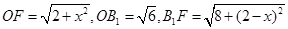 。由余弦定理可得,
。由余弦定理可得,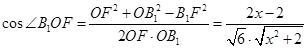 。记
。记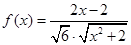 ,则
,则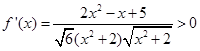 ,则
,则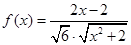 在区间
在区间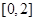 上单调递增,所以
上单调递增,所以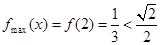 ,所以不存在点
,所以不存在点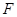 使得二面角
使得二面角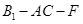 的大小为
的大小为 ,命题③不正确;
,命题③不正确;因为
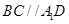 ,所以
,所以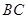 与平面
与平面 所成角等于
所成角等于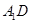 与平面
与平面 所成角。过点
所成角。过点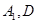 分别作
分别作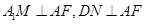 。因为
。因为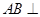 面
面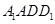 ,所以
,所以 ,从而有
,从而有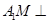 面
面 ,
,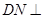 面
面 ,则
,则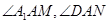 分别是
分别是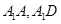 与平面
与平面 所成角,从而有
所成角,从而有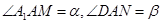 ,所以
,所以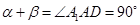 恒为定值,,命题④正确。
恒为定值,,命题④正确。
练习册系列答案
相关题目
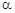 、
、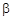 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )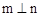 、 m
、 m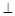
 ∥n
∥n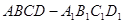 中,点
中,点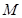 为线段
为线段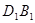 上的动点,点
上的动点,点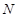 为线段
为线段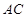 上的动点,则与线段
上的动点,则与线段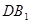 相交且互相平分的线段
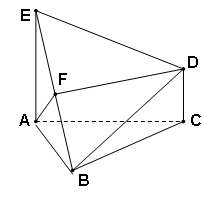
相交且互相平分的线段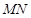 有( )
有( )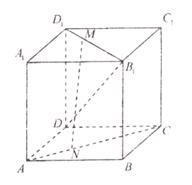


 ,在底面
,在底面 中,
中,  ,棱
,棱 ,
, 分别为
分别为 的中点。
的中点。 的值; (2)求证:
的值; (2)求证:

 -
- 中,异面直线
中,异面直线 与
与 所成角的大小为 ▲ ;
所成角的大小为 ▲ ;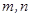 是不同的直线,
是不同的直线,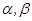 是不重合的平面,给出下面三个命题:
是不重合的平面,给出下面三个命题: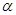 //
//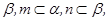 则
则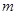 //
//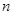 .
.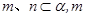 //
//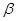 ,
,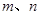 是两条异面直线,若
是两条异面直线,若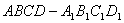 中,以顶点
中,以顶点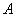 为端点的三条棱长都是
为端点的三条棱长都是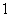 ,且它们彼此的夹角都是
,且它们彼此的夹角都是 ,则以
,则以


