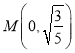题目内容
【题目】如图，已知椭圆
，
点是它的右端点，弦
过椭圆的中心
，
，
.
（1）求椭圆的标准方程；
（2）设
、
为圆上不重合的两点，
的平分线总是垂直于
轴，且存在实数
，使得
，求的最大值.
【答案】（1）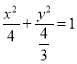
；（2）
.
【解析】
（1）先求出
的值，再求出点
的坐标，并将点的坐标代入椭圆方程，得出
的值，即可得出椭圆的标准方程；
（2）先由已知条件得出直线
和直线
的斜率互为相反数，可设直线的方程为
，将直线的方程与椭圆方程联立，求出点
的坐标，同理得出点
的坐标，利用向量的坐标运算得出实数
的表达式，再利用基本不等式可求出的最大值．
（1）依题意可知
，
，
.
又
，
，
是等腰直角三角形，
，
.又点在椭圆上，
，
，因此，所求椭圆的标准方程为；
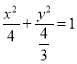（2）如下图所示：
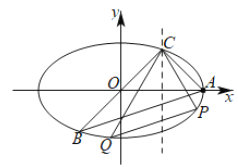
对于椭圆上两点、，
的平分线总是垂直于
轴，
与
所在直线关于直线
对称.
设
，则
，
则直线的方程为
，①
直线的方程为
，②
将①代入
，得
.③
在椭圆上，
是方程③的一个根，
，
以
替换
，得到
.
，
，
易知
，
，
，
，则
，
，
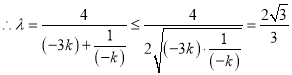当且仅当
时，即当
时，等号成立，
因此，实数的最大值为.
备战中考寒假系列答案
【题目】2019年，中华人民共和国成立70周年，为了庆祝建国70周年，某中学在全校进行了一次爱国主义知识竞赛，共1000名学生参加，答对题数（共60题）分布如下表所示：
组别 |
|
|
|
|
|
|
频数 | 10 | 185 | 265 | 400 | 115 | 25 |
答对题数
近似服从正态分布
，
为这1000人答对题数的平均值（同一组数据用该组区间的中点值作为代表）.
（1）估计答对题数在
内的人数（精确到整数位）.
（2）学校为此次参加竞赛的学生制定如下奖励方案：每名同学可以获得2次抽奖机会，每次抽奖所得奖品的价值与对应的概率如下表所示.
获得奖品的价值（单位：元） | 0 | 10 | 20 |
概率 |
|
|
|
用
（单位：元）表示学生甲参与抽奖所得奖品的价值，求的分布列及数学期望.
附：若
，则
，
，
.
【题目】某便利店计划每天购进某品牌鲜奶若干件，便利店每销售一瓶鲜奶可获利
元；若供大于求，剩余鲜奶全部退回，但每瓶鲜奶亏损
元；若供不应求，则便利店可从外调剂，此时每瓶调剂品可获利
元.
（1）若便利店一天购进鲜奶
瓶，求当天的利润
（单位：元）关于当天鲜奶需求量
（单位：瓶，
）的函数解析式；
（2）便利店记录了
天该鲜奶的日需求量（单位：瓶，）整理得下表：
日需求量 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
若便利店一天购进瓶该鲜奶，以天记录的各需求量的频率作为各需求量发生的概率，求当天利润在区间
内的概率.
