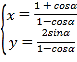题目内容
【题目】如图,已知椭圆![]()
![]() (
(![]() )与圆
)与圆![]() :
:![]() 在第一象限相交于点
在第一象限相交于点![]() ,椭圆
,椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() 都在圆
都在圆![]() 上,且线段
上,且线段![]() 为圆
为圆![]() 的直径.
的直径.

(1)求椭圆![]() 的方程;
的方程;
(2)设过点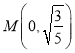 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,证明:
为坐标原点,证明:![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
【答案】(1)![]() ;(2)证明见解析,定值为
;(2)证明见解析,定值为![]() .
.
【解析】
(1)由圆的方程可得与![]() 轴的交点坐标即椭圆的焦点坐标,和圆的半径,由题意可得
轴的交点坐标即椭圆的焦点坐标,和圆的半径,由题意可得![]() 的值,再由存在求出
的值,再由存在求出![]() ,再由椭圆的定义可得椭圆的方程;
,再由椭圆的定义可得椭圆的方程;
(2)分直线的斜率存在和不存在两种情况讨论,设直线的方程与椭圆联立求出两根之和及两根之积,进而求出数量积![]() 的值为定值.
的值为定值.
解:(1)在圆![]() 的方程中,令
的方程中,令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() .
.
将圆![]() 的方程化为
的方程化为![]() ,则圆
,则圆![]() 半径为
半径为![]() ,所以
,所以![]() .
.
连结![]() ,因为点
,因为点![]() 在圆
在圆![]() 上,
上,![]() 为圆
为圆![]() 的直径,则
的直径,则![]() .
.
又![]() ,则
,则![]() .
.
据椭圆定义,![]() ,则
,则![]() .
.
从而![]() ,所以椭圆
,所以椭圆![]() 的方程是
的方程是![]() ;
;
(2)当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得
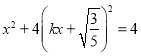 ,即
,即![]() .
.
设点![]() ,
,![]() .则
.则![]() ,
,![]() .
.
所以![]()
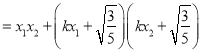
![]()
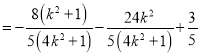
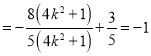 ,
,
当![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 与
与![]() 轴重合,此时点
轴重合,此时点![]() ,
,![]() ,
,![]() ,
,
综上分析,![]() 为定值.
为定值.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?