Question

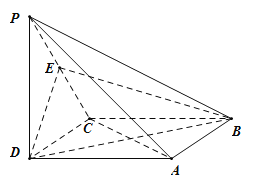
【题目】图①是一栋新农村别墅，它由上部屋顶和下部主体两部分组成．如图②，屋顶由四坡屋面构成，其中前后两坡屋面ABFE和CDEF是全等的等腰梯形，左右两坡屋面EAD和FBC是全等的三角形．点F在平面ABCD和BC上的射影分别为H，M．已知HM 5 m，BC 10 m，梯形ABFE的面积是△FBC面积的2.2倍．设∠FMH ．

（1）求屋顶面积S关于的函数关系式；

（2）已知上部屋顶造价与屋顶面积成正比，比例系数为k（k为正的常数），下部主体造价与其 高度成正比，比例系数为16 k．现欲造一栋上、下总高度为6 m的别墅，试问：当为何值时，总造价最低？

Answer 1

【答案】（1）；（2）当为时该别墅总造价最低

【解析】

（1）由题知FH⊥HM，在Rt△FHM中，所以，得△FBC的面积，从而得到屋顶面积；（2）别墅总造价为=令，求导求最值即可

（1）由题意FH⊥平面ABCD，FM⊥BC，

又因为HM 平面ABCD，得FH⊥HM．

在Rt△FHM中，HM 5，，所以．

因此△FBC的面积为．

从而屋顶面积 ．

所以S关于的函数关系式为()．

（2）在Rt△FHM中，，所以主体高度为．

所以别墅总造价为

记，，

所以，

令，得，又，所以．

列表：

		0

所以当时，有最小值．

答：当为img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/26/08/947417a4/SYS201905260820246408592582_DA/SYS201905260820246408592582_DA.003.png" width="9" height="33" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />时该别墅总造价最低．