Question

【题目】不等式对任意实数都成立，则实数的取值范围_________

Answer 1

【答案】

【解析】

根据题意，分2种情况讨论：1°若a2﹣1＝0，则a＝±1，分别验证a＝1或﹣1时，是否能保证该不等式满足对任意实数x都成立，

2°若a2﹣1≠0，不等式（a2﹣1）x2+（a﹣1）x﹣1≤0为二次不等式，结合二次函数的性质，解可得此时a的范围，综合可得答案．

根据题意，分2种情况讨论：

1°若a2﹣1＝0，则a＝±1，

当a＝1时，不等式（a2﹣1）x2+（a﹣1）x﹣1≤0为：﹣1≤0，

满足对任意实数x都成立，则a＝1满足题意，

当a＝﹣1时，不等式（a2﹣1）x2+（a﹣1）x﹣1≤0为：﹣2x≤0，

不满足对任意实数x都成立，则a＝﹣1不满足题意，

2°若a2﹣1≠0，不等式（a2﹣1）x2+（a﹣1）x﹣1≤0为二次不等式，

要保证（a2﹣1）x2+（a﹣1）x﹣1≤0对任意实数x都成立，

必须有，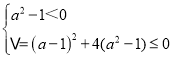

解可得：a＜1，

综合可得a≤1，

故答案为：