题目内容
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 存在极值点,求
存在极值点,求![]() 的取值范围;
的取值范围;
(2)设![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的最大整数值.
的最大整数值.
【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)求出导函数![]() ,将题目转化为解决导函数的零点问题;
,将题目转化为解决导函数的零点问题;
(2)分离参数解决![]() 恒成立,讨论函数
恒成立,讨论函数![]() 的最值即可求解.
的最值即可求解.
(1)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
因为函数![]() 存在极值点,所以
存在极值点,所以![]() 在
在![]() 上有解.
上有解.
当![]() 时,
时,![]() ,
,
所以![]() ,经检验,
,经检验,
当![]() 时,
时,![]() 得
得![]()
由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以函数![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减,符合条件函数
单调递减,符合条件函数![]() 存在极大值点,.
存在极大值点,.
所以![]() 的取值范围为
的取值范围为![]() .
.
(2)因为![]() ,所以
,所以![]() .
.
不等式![]() 在
在![]() 上恒成立,可等价转化为
上恒成立,可等价转化为![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则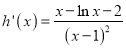 .
.
令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递增.
上单调递增.
因为![]() ,
,![]() ,
,
所以存在![]() 使
使![]() ,即
,即![]() .
.
所以当![]() 时,
时,![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() .
.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
由![]() ,得
,得![]() .
.
所以![]() ,
,
所以![]() ,所以
,所以![]() 的最大整数值为3.
的最大整数值为3.

练习册系列答案
相关题目
【题目】某芯片公司为制定下一年的研发投入计划,需了解年研发资金投入量![]() (单位:亿元)对年销售额
(单位:亿元)对年销售额![]() (单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①
(单位:亿元)的影响.该公司对历史数据进行对比分析,建立了两个函数模型:①![]() ,②
,②![]() ,其中
,其中![]() 均为常数,
均为常数,![]() 为自然对数的底数.
为自然对数的底数.

现该公司收集了近12年的年研发资金投入量![]() 和年销售额
和年销售额![]() 的数据,
的数据,![]() ,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令
,并对这些数据作了初步处理,得到了右侧的散点图及一些统计量的值.令![]()
![]()
![]() ,经计算得如下数据:
,经计算得如下数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)设![]() 和
和![]() 的相关系数为
的相关系数为![]() ,
,![]() 和
和![]() 的相关系数为
的相关系数为![]() ,请从相关系数的角度,选择一个拟合程度更好的模型;
,请从相关系数的角度,选择一个拟合程度更好的模型;
(2)(i)根据(1的选择及表中数据,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(ii)若下一年销售额![]() 需达到90亿元,预测下一年的研发资金投入量
需达到90亿元,预测下一年的研发资金投入量![]() 是多少亿元?
是多少亿元?
附:①相关系数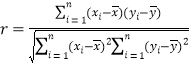 ,回归直线
,回归直线![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: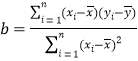 ,
,![]() ;
;
② 参考数据:![]() ,
,![]() ,
,![]() .
.