题目内容
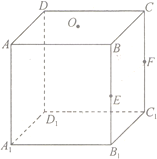
【题目】如图，在正方体
中，点
，
分别为棱
，
的中点，点
为上底面的中心，过，，三点的平面把正方体分为两部分，其中含
的部分为
，不含的部分为
，连结和的任一点
，设
与平面
所成角为
，则
的最大值为
A. 
B. 
C. 
D. 
【答案】B
【解析】
连结
.可证平行四边形
即为截面. 五棱柱
为
，三棱柱
为
，设
点为的任一点，过点作底面
的垂线，垂足为
，连结
，则
即为
与平面所成的角，所以
.
进而得到
的最大值.
连结.因为
平面
.所以过
的平面与平面的交线一定是过点
且与平行的直线.过点作
交
于点
，交
于
点，则
，连结
，
.则平行四边形即为截面.则五棱柱为，三棱柱为，设点为的任一点，过点作底面的垂线，垂足为，连结，则即为与平面所成的角，所以.
因为
，要使
的正弦值最大，必须
最大，最小，当点与点重合时符合题意.故
.故选B.
练习册系列答案
相关题目
【题目】某省开展“精准脱贫，携手同行”的主题活动，某贫困县统计了100名基层干部走访贫困户的数量，并将走访数量分成5组，统计结果见下表.
走访数量区间 | 频数 | 频率 |
| b | |
| 10 | |
| 38 | |
| a | 0.27 |
| 9 | |
总计 | 100 | 1.00 |
（1）求a与b的值；
（2）根据表中数据，估计这100名基层干部走访数量的中位数（精确到个位）；
（3）如果把走访贫困户不少于35户视为“工作出色”，按照分层抽样，从“工作出色”的基层干部中抽取4人，再从这4人中随机抽取2人，求其中有1人走访贫困户不少于45户的概率.