题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的偶函数,其图象关于点
上的偶函数,其图象关于点![]() 对称.以下关于
对称.以下关于![]() 的结论:①
的结论:①![]() 是周期函数;②
是周期函数;②![]() 满足
满足![]() ;③
;③![]() 在
在![]() 单调递减;④
单调递减;④![]() 是满足条件的一个函数.其中正确结论的个数是( )
是满足条件的一个函数.其中正确结论的个数是( )
A.4B.3C.2D.1
【答案】B
【解析】
题目中条件:![]() 可得
可得![]() 知其周期,利用奇函数图象的对称性,及函数图象的平移变换,可得函数的对称中心,结合这些条件可探讨函数的奇偶性,及单调性.
知其周期,利用奇函数图象的对称性,及函数图象的平移变换,可得函数的对称中心,结合这些条件可探讨函数的奇偶性,及单调性.
解:对于①:![]() ,其图象关于点
,其图象关于点![]() 对称
对称![]()
所以![]() ,
,
![]() 函数
函数![]() 是周期函数且其周期为4,故①正确;
是周期函数且其周期为4,故①正确;
对于②:由①知,对于任意的![]() ,都有
,都有![]() 满足
满足![]() ,
,
函数是偶函数,即![]() ,故②正确.
,故②正确.
对于③:反例:如图所示的函数,关于![]() 轴对称,
轴对称,
图象关于点![]() 对称,函数的周期为4,但是
对称,函数的周期为4,但是![]() 在
在![]() 上不是单调函数,故③不正确;
上不是单调函数,故③不正确;
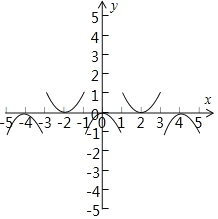
对于④:![]() 是定义在
是定义在![]() 上的偶函数,其图象关于点
上的偶函数,其图象关于点![]() 对称的一个函数,故④正确.
对称的一个函数,故④正确.
故选:![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
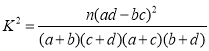 (其中
(其中![]() ).
).