题目内容
18.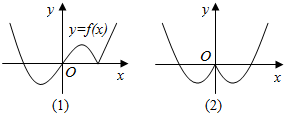 已知如图(1)的图象对应的函数为y=f(x),给出①y=f(|x|);②y=|f(x)|-a;③y=-f(|x|);④y=f(-|x|).⑤y=|f(|x|)|-a,则如图(2)的图象对应的函数可能是五个式子中的( )
已知如图(1)的图象对应的函数为y=f(x),给出①y=f(|x|);②y=|f(x)|-a;③y=-f(|x|);④y=f(-|x|).⑤y=|f(|x|)|-a,则如图(2)的图象对应的函数可能是五个式子中的( )| A. | ④ | B. | ②④ | C. | ①② | D. | ②③④⑤ |
分析 由图(2)知,图象对应的函数是偶函数,对选项一一利用排除法分析可得答案.
解答 解:由图(2)知,图象对应的函数是偶函数,
对于①,当x>0时,y=f(|x|)=y=f(x),其图象在y轴右侧与图一的相同,不合题意,故排除①.
对于②,当x>0时,对应的函数是y=f(x)-a,是把(1)中图象位于y轴右侧的部分向下平移a个单位得到的,显然不正确,故排除②.
对于③,当x>0时,对应的函数是y=-f(x),是把(1)中图象位于y轴右侧的部分关于x轴对称得到的,显然不正确,故排除③.
对于④,当x>0时,对应的函数是y=f(-x),是把(1)中图象位于y轴左侧的部分关于y轴对称得到的,满足条件.
对于⑤,当x>0时,对应的函数是y=|f(x)|-a,是把(1)中图象位于y轴右侧的部分向下平移a个单位得到的,显然不正确,故排除⑤,
故选:A.
点评 本题考查函数的图象、函数的图象与图象变化,考查学生读图能力,分析问题解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若f(x)=$\frac{1}{2}$x2-ax+alnx在(0,+∞)上单调增,则实数a的取值范围为( )
| A. | (0,+∞) | B. | (-∞,4] | C. | [0,4] | D. | (4,+∞) |
3.已知x,y满足约束条件$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤2}\\{y≥0}\end{array}}\right.$,则z=2x+y的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.函数f(x)=$\sqrt{x-2}+\frac{1}{{ln({3-x})}}$的定义域为( )
| A. | [2,3) | B. | (2,3) | C. | [2,+∞) | D. | (-∞,3] |