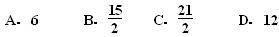题目内容
若点A,B,C是半径为2的球面上三点,且AB=2,则球心到平面ABC的距离最大值为
A.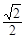 | B.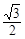 | C.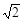 | D.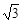 |
D
分析:当截面是以AB为直径的圆时,球心O到平面ABC的距离最大,可求得球心O到平面ABC的距离最大值为
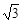 .
.解:因为当截面是以AB为直径的圆时,
球心到过A、B两点的平面的距离最大.
设截面圆的圆心为O1,球心为O,
则△OO1A是以∠OO1A=90°的直角三角形,
且AO1=1,AO=2,球心到截面的距离OO1=
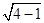 =
=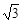 .
.所以:截面圆半径为1,球心到截面的距离为:
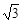 .
.故选D.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
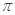
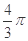
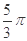


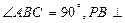 平面ABC,AB=BC=2
平面ABC,AB=BC=2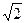 ,PB=2,则点B到平面PAC的距离是
,PB=2,则点B到平面PAC的距离是  四面体
四面体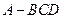 中,共顶点
中,共顶点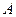 的三条棱两两互相垂直,且
的三条棱两两互相垂直,且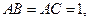 ,
,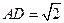 若四
若四 面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。
面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。 
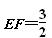 ,则该多面体的体积为( )
,则该多面体的体积为( )