题目内容
已知常数a、b都是正整数,函数f(x)=
(x>0),数列{an}满足a1=a,
=f(
)(n∈N*)
(1)求数列{an}的通项公式;
(2)若a=8b,且等比数列{bn}同时满足:①b1=a1,b2=a5;②数列{bn}的每一项都是数列{an}中的某一项.试判断数列{bn}是有穷数列或是无穷数列,并简要说明理由;
(3)对问题(2)继续探究,若b2=am(m>1,m是常数),当m取何正整数时,数列{bn}是有穷数列;当m取何正整数时,数列{bn}是无穷数列,并说明理由.
| x |
| bx+1 |
| 1 |
| an+1 |
| 1 |
| an |
(1)求数列{an}的通项公式;
(2)若a=8b,且等比数列{bn}同时满足:①b1=a1,b2=a5;②数列{bn}的每一项都是数列{an}中的某一项.试判断数列{bn}是有穷数列或是无穷数列,并简要说明理由;
(3)对问题(2)继续探究,若b2=am(m>1,m是常数),当m取何正整数时,数列{bn}是有穷数列;当m取何正整数时,数列{bn}是无穷数列,并说明理由.
(1)∵
=f(
)=
=
∴an+1=an+b,∴数列{an}是以b为公差的等差数列
∵a1=a,∴an=a+(n-1)b
(2)当a=8b时,an=(n+7)b
∴b1=8b,b2=12b,∴q=
,∴bn=8b•(
)n-1
∴b3=18b,b4=27b,b5=
b
显然,
不是整数,即b5∉{an},∴{bn}是项数最多为4的有穷数列
(3)∵b2=(m+7)b,∴q=
,此时bn=8(
)n-1b
i)当m=8k+1(k∈N)时,
=k+1为正整数,
此时{bn}中每一项均为{an}中的项,∴{bn}为无穷数列;
ii)当m=8k+5(k∈N)时,
=
此时当n=1,2,3,4,8(
)n-1为大于8的正整数,
但n=5时,8(
)4不是正整数,∴此时{bn}是项数最多为4的有穷数列;
iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)时,
此时
为分母是4或8的最简分数,
只有当n=1,2时,8(
)n-1才是大于8的正整数,
而当n≥3时,8(
)n-1均为分数,∵{bn}仅有两项,∴此时{bn}不能构成等比数列.
| 1 |
| an+1 |
| 1 |
| an |
| ||
b
|
| 1 |
| an+b |
∴an+1=an+b,∴数列{an}是以b为公差的等差数列
∵a1=a,∴an=a+(n-1)b
(2)当a=8b时,an=(n+7)b
∴b1=8b,b2=12b,∴q=
| 3 |
| 2 |
| 3 |
| 2 |
∴b3=18b,b4=27b,b5=
| 81 |
| 2 |
显然,
| 81 |
| 2 |
(3)∵b2=(m+7)b,∴q=
| m+7 |
| 8 |
| m+7 |
| 8 |
i)当m=8k+1(k∈N)时,
| m+7 |
| 8 |
此时{bn}中每一项均为{an}中的项,∴{bn}为无穷数列;
ii)当m=8k+5(k∈N)时,
| m+7 |
| 8 |
| 2k+3 |
| 2 |
此时当n=1,2,3,4,8(
| 2k+3 |
| 2 |
但n=5时,8(
| 2k+3 |
| 2 |
iii)当m=8k+2,+3,+4,+6,+7,+8(k∈N)时,
此时
| m+7 |
| 8 |
只有当n=1,2时,8(
| 2k+3 |
| 2 |
而当n≥3时,8(
| 2k+3 |
| 2 |

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
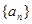 是公比为
是公比为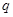 的等比数列,推导
的等比数列,推导 项公式.
项公式.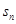 为等比数列
为等比数列 的前n项和,已知
的前n项和,已知
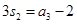 ,则公比q = ( ).
,则公比q = ( ).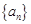 的前n项和
的前n项和 与通项
与通项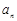 满足
满足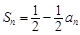 .
. ,求
,求 ;
; ,求
,求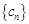 的前n项和
的前n项和 .
.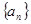 公比
公比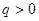 ,若
,若 ,
,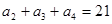 ,则
,则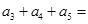 .
.