题目内容
设项数为奇数的等差数列，奇数项之和为44，偶数项之和为33，求这个数列的中间项及项数．
设等差数列{an}项数为2n+1，
S奇=a1+a3+…+a2n+1=
=(n+1)an+1，
S偶=a2+a4+a6+…+a2n=
=nan+1，
∴
=
=
，解得n=3，
∴项数2n+1=7，
又因为S奇-S偶=an+1=a中，
所以a4=S奇-S偶=44-33=11，
所以中间项为11．
S奇=a1+a3+…+a2n+1=
| (n+1)(a1+a2n+1) |
| 2 |
S偶=a2+a4+a6+…+a2n=
| n(a2+a2n) |
| 2 |
∴
| S奇 |
| S偶 |
| n+1 |
| n |
| 44 |
| 33 |
∴项数2n+1=7，
又因为S奇-S偶=an+1=a中，
所以a4=S奇-S偶=44-33=11，
所以中间项为11．
练习册系列答案
阅读快车系列答案
相关题目
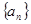中，
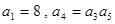，则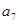
= ( )
