题目内容
16.已知动圆过定点A(0,12),且在x轴上截得的弦MN的长为1,设动圆圆心的轨道为l.(1)求动圆圆心的轨迹L的方程;
(2)已知直线y=a交曲线L于A、B两点,若曲线L上存在点C,使得∠ACB为直角,求a的取值范围;
(3)设轨迹L的焦点为F、A、B为轨迹L上的两个动点,且满足∠AFB=120°,过弦AB的中点M作直线y=-14的垂线MN,垂足为N,试求|MN||AB|的最大值.
分析 (1)设圆心的坐标为(x,y),由题意可得√x2+(y−12)2=√y2+14,两边平方化简即可得到轨迹方程;
(2)可知A(-√a,a),B(√a,a),设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得→AC•→BC=0.即可得到a的取值范围;
(3)设AF=a,BF=b,由抛物线定义,2MN=a+b.再由余弦定理可得|AB|2=a2+b2-2abcos120°,进而根据a+b≥2√ab,求得|AB|的范围,进而可得答案.
解答  解:(1)设圆心的坐标为(x,y),由题意可得
解:(1)设圆心的坐标为(x,y),由题意可得
√x2+(y−12)2=√y2+14,
化简可得,y=x2,
即为动圆圆心的轨迹L的方程;
(2)如图所示,可知A(-√a,a),B(√a,a),
设C(m,m2),→AC=(m+√a,m2-a),→BC=(m-√a,m2-a).
∵该抛物线上存在点C,使得∠ACB为直角,
∴→AC•→BC=(m+√a)(m-√a)+(m2-a)2=0.
化为m2-a+(m2-a)2=0.
∵m≠±√a,∴m2=a-1≥0,解得a≥1.
∴a的取值范围为[1,+∞).
(3)设AF=a,BF=b,由抛物线定义,2MN=a+b.
由余弦定理,|AB|2=a2+b2-2abcos120°=(a+b)2-ab,
再由a+b≥2√ab,得到ab≤(a+b)24,
即有|AB|≥√32(a+b).即|MN||AB|≤√33.
所以|MN||AB|的最大值为√33.
点评 本题考查轨迹方程的求法,向量垂直的条件,余弦定理和基本不等式的运用,考查了学生综合分析问题和解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.某厂大量生产一种小零件,经抽样检验知道其次品率是1%,现把这种零件中6件装成一盒,那么该盒中恰好含一件次品的概率是( )
| A. | (99100)2 | B. | 0.01 | ||
| C. | C161100•(1-1100)5 | D. | C26(1100)2•(1-1100)4 |
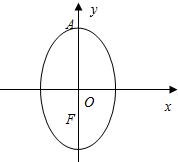 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.