题目内容
5.已知椭圆Q:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右顶点P(2,0),离心率为$\frac{\sqrt{3}}{2}$,O为坐标原点.(1)求椭圆O的方程;
(2)设A、B、M是椭圆上的三点,$\overrightarrow{OM}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{4}{5}$$\overrightarrow{OB}$,点N为线段AB的中点,C、D两点的坐标分别为(-$\frac{\sqrt{6}}{2}$,0)、($\frac{\sqrt{6}}{2}$,0),求证:|NC|+|ND|=2$\sqrt{2}$.
分析 (1)利用椭圆Q:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右顶点P(2,0),离心率为$\frac{\sqrt{3}}{2}$,求出a,b后可得椭圆的方程;
(2)设出A,B的坐标,由$\overrightarrow{OM}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{4}{5}$$\overrightarrow{OB}$得到M的坐标,把M的坐标代入椭圆方程得到$\frac{1}{4}$($\frac{3}{5}$x1+$\frac{4}{5}$x2)2+($\frac{3}{5}$y1+$\frac{4}{5}$y2)2=1,再由A,B在椭圆上整理可得点N在椭圆$\frac{{x}^{2}}{2}+2{y}^{2}=1$上,且C,D为该椭圆的两个焦点坐标,则答案可求.
解答 (1)解:∵椭圆Q:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)右顶点P(2,0),离心率为$\frac{\sqrt{3}}{2}$,
∴a=2,$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴c=$\sqrt{3}$,b=1,
∴椭圆Q的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)证明:设A(x1,y1),B(x2,y2),则$\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}$=1,$\frac{{{x}_{2}}^{2}}{4}+{{y}_{2}}^{2}=1$ ①,
由$\overrightarrow{OM}$=$\frac{3}{5}$$\overrightarrow{OA}$+$\frac{4}{5}$$\overrightarrow{OB}$,得M($\frac{3}{5}$x1+$\frac{4}{5}$x2,$\frac{3}{5}$y1+$\frac{4}{5}$y2),
又点M在椭圆Q:$\frac{{x}^{2}}{4}+{y}^{2}=1$上,
则有$\frac{1}{4}$($\frac{3}{5}$x1+$\frac{4}{5}$x2)2+($\frac{3}{5}$y1+$\frac{4}{5}$y2)2=1②,
综合①、②得:$\frac{{x}_{1}{x}_{2}}{4}$+y1y2=0.
又线段AB的中点为N($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$),
且$\frac{1}{4}$($\frac{{x}_{1}+{x}_{2}}{2}$)2+($\frac{{y}_{1}+{y}_{2}}{2}$)2=$\frac{1}{4}$($\frac{{{x}_{1}}^{2}}{4}+{{y}_{1}}^{2}$)+$\frac{1}{4}$($\frac{{{x}_{2}}^{2}}{4}+{{y}_{2}}^{2}$)+$\frac{1}{2}$($\frac{{x}_{1}{x}_{2}}{4}$+y1y2)=$\frac{1}{2}$
上式表明,点N在椭圆$\frac{{x}^{2}}{2}+2{y}^{2}=1$上,且该椭圆的两个焦点恰好为(-$\frac{\sqrt{6}}{2}$,0)、($\frac{\sqrt{6}}{2}$,0),两点,
由椭圆定义有:|NC|+|ND|=2$\sqrt{2}$.
点评 本题考查了椭圆方程的求法,主要考查了直线与椭圆的位置关系的应用,训练了“设而不求”的数学解题思想方法,圆锥曲线的特点是计算量比较大,要求考生具备较强的运算推理的能力,是压轴题.

| A. | 15π | B. | $\frac{15π}{4}$ | C. | $\sqrt{15}$ π | D. | 6π |
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a,b大小关系不能判断 |
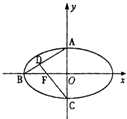 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.