题目内容
【题目】某工厂修建一个长方体无盖蓄水池，其容积为4 800立方米，深度为3米．池底每平方米的造价为150元，池壁每平方米的造价为120元．设池底长方形长为x米．
（1）求底面积，并用含x的表达式表示池壁面积；
（2）怎样设计水池能使总造价最低?最低造价是多少?
【答案】（1)1600,
（平方米）；（2）池底设计为边长40米的正方形时总造价最低，最低造价为268800元.
【解析】
（1）根据题意，由于修建一个长方体无盖蓄水池，
其容积为4 800立方米，深度为3米．
可得底面积为1600，池壁面积s=
.
（2）同时池底每平方米的造价为150元，池壁每平方米的造价为120元．
设池底长方形长为x米，
则可知总造价s=
,x=40时，
则
.
故可知当x=40时，则有可使得总造价最低,
最低造价是268800元.
导学教程高中新课标系列答案
【题目】某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
（1）分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；
（2）求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精确到0.01）
附：
.
【题目】十八大以来，我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源产品年销售 | 1.6 | 6.2 | 17.7 | 33.1 | 55.6 |
（1）请画出上表中年份代码
与年销量
的数据对应的散点图，并根据散点图判断.
与
中哪一个更适宜作为年销售量关于年份代码的回归方程类型；
（2）根据（Ⅰ）的判断结果及表中数据，建立关于的回归方程，并预测2019年某新能源产品的销售量（精确到0.01）.
参考公式：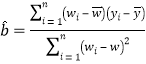
，
.
参考数据：
，
，
，
，
，
，
，其中
.
【题目】总体由编号为01，02，03，
，49，50的50个个体组成，利用随机数表（以下选取了随机数表中的第1行和第2行）选取5个个体，选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取，则选出来的第4个个体的编号为（ ）
78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
A. 05 B. 09 C. 07 D. 20
