题目内容
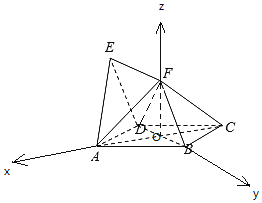
【题目】如图,已知四边形ABCD与四边形BDEF均为菱形,![]() ,且
,且![]()

![]() 求证:
求证:![]() 平面BDEF;
平面BDEF;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见证明;(2)![]() .
.
【解析】
![]() 设AC、BD交于点O,连结OF、DF,推导出
设AC、BD交于点O,连结OF、DF,推导出![]() ,
,![]() ,
,![]() ,由此能证明
,由此能证明![]() 平面BDEF.
平面BDEF.
![]() 以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角
以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
![]() 设AC、BD交于点O,连结OF、DF,
设AC、BD交于点O,连结OF、DF,
![]() 四边形ABCD与四边形BDEF均为菱形,
四边形ABCD与四边形BDEF均为菱形,![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 四边形ABCD与四边形BDEF均为菱形,
四边形ABCD与四边形BDEF均为菱形,
![]() ,
,
![]() ,
,![]() 平面BDEF.
平面BDEF.
![]() ,
,![]() ,
,![]() 平面ABCD,
平面ABCD,
![]() 以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
以OA为x轴,OB为y轴,OF为z轴,建立空间直角坐标系,
设![]() ,则
,则![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
![]() ,
,![]() 1,
1,![]() ,
,
![]() ,
,
设平面ABF的法向量![]() y,
y,![]() ,
,
则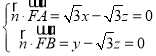 ,取
,取![]() ,得
,得![]() ,
,
设平面BCF的法向量![]() y,
y,![]() ,
,
则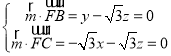 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,由图可知为钝角
,由图可知为钝角
则![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度,![]() 为答对该题的人数,
为答对该题的人数,![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
学生 编号 题号 | 1 | 2 | 3 | 4 | 5 |
1 | × | √ | √ | √ | √ |
2 | √ | √ | √ | √ | × |
3 | √ | √ | √ | √ | × |
4 | √ | √ | √ | × | × |
5 | √ | √ | √ | √ | √ |
6 | √ | × | × | √ | × |
7 | × | √ | √ | √ | × |
8 | √ | × | × | × | × |
9 | √ | √ | × | × | × |
10 | √ | √ | √ | √ | × |
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;
题号 | 1 | 2 | 3 | 4 | 5 |
实测答对人数 | |||||
实测难度 |
(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度,![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度估合理,否则为不合理.判断本次测试的难度预估是否合理.
【题目】已知某市2015年全年空气质量等级如表1所示.
表1
空气质量等级(空气质量指数(AQI)) | 频数 | 频率 |
优( | 83 | 22.8% |
良( | 121 | 33.2% |
轻度污染( | 68 | 18.6% |
中度污染( | 49 | 13.4% |
重度污染( | 30 | 8.2% |
严重污染( | 14 | 3.8% |
合计 | 365 | 100% |
2016年5月和6月的空气质量指数如下:
5月 240 80 56 53 92 126 45 87 56 60
191 62 55 58 56 53 89 90 125 124
103 81 89 44 34 53 79 81 62 116
88
6月 63 92 110 122 102 116 81 163 158 76
33 102 65 53 38 55 52 76 99 127
选择合适的统计图描述数据,并回答下列问题:
(1)分析该市2016年6月的空气质量情况.
(2)比较该市2016年5月和6月的空气质量,哪个月的空气质量较好?
(3)比较该市2016年6月与该市2015年全年的空气质量,2016年6月的空气质量是否好于去年?
