Question

【题目】在直角坐标系中，直线，圆．以原点为极点，轴的正半轴为极轴建立极坐标系．

（1）求的极坐标方程；

（2）若直线的极坐标方程为，设与的交点为、，求.

Answer 1

【答案】（1）；（2）.

【解析】

（1）由可得出曲线的极坐标方程；

（2）解法一：求出直线的普通方程，利用点到直线的距离公式计算出圆的圆心到直线的距离，再利用勾股定理计算出；

解法二：设点、的极坐标分别为、，将圆的方程化为极坐标方程，并将直线的方程与圆的极坐标方程联立，得出关于的二次方程，列出韦达定理，可得出，从而计算出.

（1）由直线，可得的极坐标方程为；

（2）解法一：由直线的极坐标方程为，

得直线的直角坐标方程为，即.

圆的圆心坐标为，半径为，

则圆心到直线的距离，；

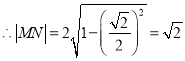解法二：圆的普通方程为，

化为极坐标方程得，

设点、的极坐标分别为、，

将直线的极坐标方程代入圆的极坐标方程得，，

由韦达定理得，，

因此，.