题目内容
【题目】已知椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(2)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .设
.设![]() 为原点,判断直线
为原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ,离心率
,离心率![]() (2)直线
(2)直线![]() 与直线
与直线![]() 平行,理由见解析.
平行,理由见解析.
【解析】
(1)将P点代入椭圆方程,可得a的值,结合离心率的公式可得离心率的值;
(2)设直线![]() ,
,![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,![]() ,分别求出
,分别求出![]() ,
,![]() ,根据斜率公式以及两直线的位置关系与斜率的关系可得答案.
,根据斜率公式以及两直线的位置关系与斜率的关系可得答案.
解:(1)由椭圆方程椭圆![]() 过点
过点![]() ,可得
,可得![]() .
.
∴![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() ,离心率
,离心率![]() .
.
(2)直线![]() 与直线
与直线![]() 平行.证明如下:
平行.证明如下:
设直线![]() ,
,![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,
由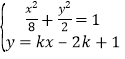 得
得![]() ,
,
∴![]() ,∴
,∴![]() ,同理
,同理![]() ,
,
∴![]() ,
,
由![]() ,
,![]() ,有
,有![]() ,
,
∵![]() 在第四象限,∴
在第四象限,∴![]() ,且
,且![]() 不在直线
不在直线![]() 上.∴
上.∴![]() ,
,
又![]() ,故
,故![]() ,∴直线
,∴直线![]() 与直线
与直线![]() 平行.
平行.

练习册系列答案
相关题目
【题目】工厂车间某部门有8个小组,在一次技能考试中成绩情况分析如下:
小组 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
大于90分人数 | 6 | 6 | 7 | 3 | 5 | 3 | 3 | 7 |
不大于90分人数 | 39 | 39 | 38 | 42 | 40 | 42 | 42 | 38 |
(1)求90分以上人数![]() 对小组序号
对小组序号![]() 的线性回归方程;
的线性回归方程;
附:回归方程为![]() ,其中
,其中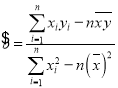 ,
,![]() .本题
.本题![]() ,
,![]() .
.
(2)能否在犯错误的概率不超过0.01的前提下认为7组与8组的成绩是否优秀(大于90分)与小组有关系.附部分临界值表:
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
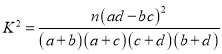 .
.
