题目内容
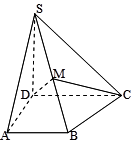
如图:已知长方体 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高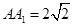 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点.
(1)求证: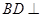 平面
平面 ;
;
(2)求证: ∥平面
∥平面 ;
;
(3)求三棱锥 的体积.
的体积.

 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高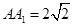 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点. (1)求证:
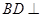 平面
平面 ;
;(2)求证:
 ∥平面
∥平面 ;
;(3)求三棱锥
 的体积.
的体积.
(1)证明见解析;(2)证明见解析;(3)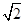 .
.
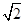 .
.试题分析:(1)要证
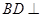 平面
平面 ,就要在平面
,就要在平面 内找两条与
内找两条与 垂直的相交直线,由于
垂直的相交直线,由于 是正方形,因此有
是正方形,因此有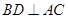 ,而在长方体中,侧棱
,而在长方体中,侧棱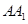 与底面垂直,从而一定有
与底面垂直,从而一定有 ,两条直线找到了;(2)要证
,两条直线找到了;(2)要证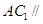 平面
平面 ,就应该在平面内找一条直线与
,就应该在平面内找一条直线与 平行,观察图形发现平面
平行,观察图形发现平面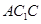 与平面
与平面 相交于直线
相交于直线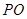 (
( 是
是 与
与 的交点),那么
的交点),那么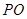 就是我们要找的平行线,这个根据中位线定理可得;(3)求三梭锥
就是我们要找的平行线,这个根据中位线定理可得;(3)求三梭锥 的体积,一般是求出其底
的体积,一般是求出其底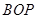 的面积
的面积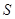 和高(顶点
和高(顶点 到底面
到底面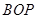 的距离)
的距离)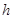 ,利用体积公式
,利用体积公式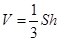 得到结论,本题中点
得到结论,本题中点 到底面
到底面 的距离,即过
的距离,即过 到底面
到底面 垂直的直线比较难以找到,考虑到三棱锥的每个面都是三角形,因此我们可以换底,即以其他面为底面,目的是高易求,由于长方体
垂直的直线比较难以找到,考虑到三棱锥的每个面都是三角形,因此我们可以换底,即以其他面为底面,目的是高易求,由于长方体 的底面
的底面 是正方形,其中垂直关系较多,可证
是正方形,其中垂直关系较多,可证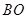
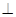 平面
平面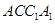 ,即
,即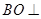 平面
平面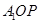 ,因此以
,因此以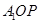 为底,
为底,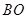 就是高,体积可得.
就是高,体积可得.试题解析:(1)
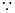 底面
底面 是边长为正方形,
是边长为正方形,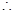
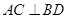
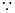
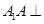 底面
底面 ,
,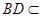 平面
平面
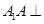
 3分
3分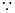
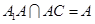 ,
,
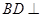 平面
平面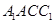 5分
5分(2)连结
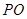 ,
,
 为
为 的中点,
的中点, 为
为 的中点
的中点
 ∥
∥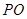 , 7分
, 7分又
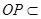 平面
平面 ,
,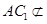 平面
平面
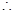
 ∥平面
∥平面 10分
10分(3)
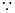
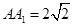 ,
,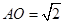 ,
,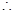
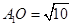 ,
,同样计算可得
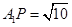 ,
,
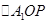 为等腰三角形, 12分
为等腰三角形, 12分
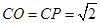 ,
,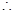
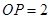 ,
,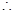 等腰三角形
等腰三角形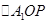 的高为
的高为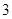
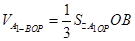
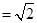 14分
14分
练习册系列答案
相关题目
 ,其表面展开图是三角形
,其表面展开图是三角形 ,如图,求△
,如图,求△ .
.
 中,
中, ,
,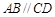 ,
,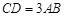 ,平面
,平面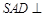 平面
平面 ,
,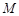 是线段
是线段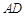 上一点,
上一点,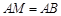 ,
,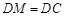 ,
,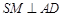 .
.
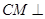
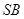 ;
;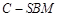 与四棱锥
与四棱锥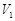 与
与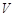 ,求
,求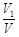 的值.
的值.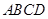 中,
中,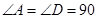 °,
°,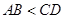 ,
,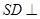 平面
平面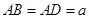 ,
,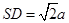 ,设
,设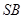 的中点为
的中点为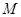 ,
,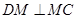 .
.
 平面
平面 ;
; 的体积.
的体积.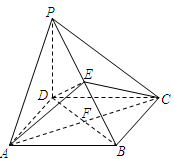
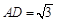 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.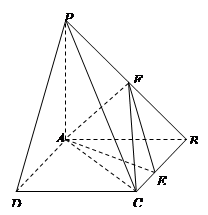
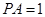 ,求证:
,求证: ;
;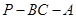 的大小为
的大小为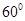 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥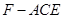 的体积为
的体积为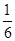 .
.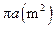 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为 .
,且它的侧面展开图是一个半圆,则圆锥的底面半径为 . ,高为2,则直三棱柱的外接球的表面积为( )
,高为2,则直三棱柱的外接球的表面积为( )



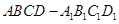 的8个顶点都在球
的8个顶点都在球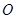 的表面上,
的表面上,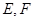 分别是棱
分别是棱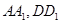 的中点,点
的中点,点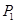 ,
,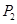 分别是线段
分别是线段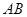 ,
,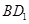 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段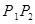 平行于平面
平行于平面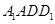 ,则
,则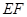 被球
被球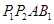 的体积的最大值是
的体积的最大值是