题目内容
如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.
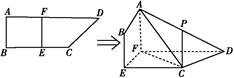
(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.

(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A
 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
(1)见解析 (2)当x=3时,  有最大值,最大值为3
有最大值,最大值为3
 有最大值,最大值为3
有最大值,最大值为3(1)证明:取AF的中点Q,
连接QE、QP,
则QP

 DF,
DF,又DF=4,EC=2,且DF∥EC,
所以QP
 EC,
EC,即四边形PQEC为平行四边形,
所以CP∥EQ,
又EQ?平面ABEF,CP?平面ABEF,
故CP∥平面ABEF.
(2)解:因为平面ABEF⊥平面EFDC,
平面ABEF∩平面EFDC=EF,
又AF⊥EF,所以AF⊥平面EFDC.
由已知BE=x,所以AF=x(0<x≤4),FD=6-x.
故
 =
= ·
· ·2·(6-x)·x
·2·(6-x)·x=
 (6x-x2)
(6x-x2)=
 [-(x-3)2+9]
[-(x-3)2+9]=-
 (x-3)2+3,
(x-3)2+3,∴当x=3时,
 有最大值,最大值为3.
有最大值,最大值为3.
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 为圆
为圆 的直径,点
的直径,点 .
.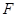 在圆
在圆 ,矩形
,矩形 所在的平面和圆
所在的平面和圆 ,
, .
.
 的中点为
的中点为 ,求证:
,求证: 平面
平面 ;
; 的体积.
的体积.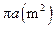 ,且它的侧面展开图是一个半圆,则圆锥的底面半径为 .
,且它的侧面展开图是一个半圆,则圆锥的底面半径为 .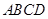 ,
,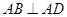 ,
,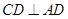 ,
,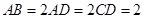 沿
沿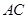 折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积
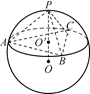
折叠成三棱锥,当三棱锥体积最大时,求此时三棱锥外接球的体积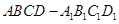 的8个顶点都在球
的8个顶点都在球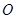 的表面上,
的表面上,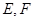 分别是棱
分别是棱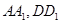 的中点,点
的中点,点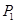 ,
,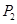 分别是线段
分别是线段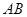 ,
,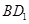 (不包括端点)上的动点,且线段
(不包括端点)上的动点,且线段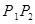 平行于平面
平行于平面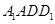 ,则
,则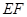 被球
被球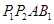 的体积的最大值是
的体积的最大值是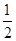
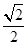

 π
π