题目内容
圆锥的表面积是底面积的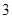 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )
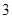 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )A. | B. | C. | D. |

试题分析:圆锥的表面积是其侧面积与底面积之和,根据题意有侧面积是底面积的2倍.又因为圆锥的侧面展开图是扇形,其圆心角
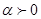 ,半径为
,半径为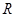 ,且其弧长等于圆锥底面周长,所以
,且其弧长等于圆锥底面周长,所以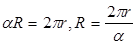 ,根据扇形面积公式有
,根据扇形面积公式有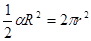 ,代入
,代入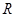 ,得
,得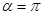 .
.
练习册系列答案
相关题目
题目内容
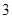 倍,那么该圆锥的侧面展开图扇形的圆心角为( )
倍,那么该圆锥的侧面展开图扇形的圆心角为( )A. | B. | C. | D. |

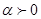 ,半径为
,半径为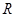 ,且其弧长等于圆锥底面周长,所以
,且其弧长等于圆锥底面周长,所以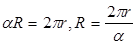 ,根据扇形面积公式有
,根据扇形面积公式有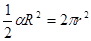 ,代入
,代入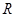 ,得
,得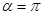 .
.