Question

【题目】△ABC的三内角A，B，C所对的边分别为a，b，c，若cosA=cosB，b=，c=4，M，N是边AC上的两个动点，且AM=2CN，则的最大值为______．

Answer 1

【答案】

【解析】

由b=结合正弦定理可得，sinB=sinA，然后再由二倍角公式及已知关系可求△ABC为直角三角形，C=，然后求出，建立直角坐标系，利用向量的数量积的坐标表示及二次函数的性质即可求解。

解：由b=可得，sinB=sinA，

∵cosA= cosB，

∴sinAcosA=sinBcosB，

即sin2A=sin2B，

∵0＜2A，2B＜2π，

∴2A=2B或2A+2B=π，

∴A=B，或A+B=

∵a≠b

∴A≠B

，

∴△ABC为直角三角形，C=，

∵b=，c=4，

∴b=，=2

建立如下图所示的直角坐标系，

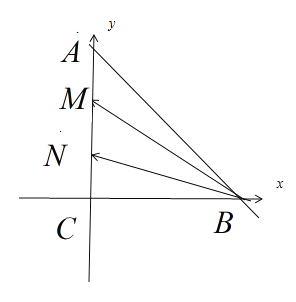
设N（0，t）则M

则

当时， 取得最大值。