题目内容
已知数列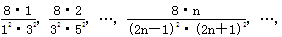 Sn为该数列的前n项和,计算得
Sn为该数列的前n项和,计算得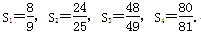
观察上述结果,推测出Sn(n∈N*),并用数学归纳法加以证明.
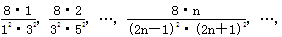 Sn为该数列的前n项和,计算得
Sn为该数列的前n项和,计算得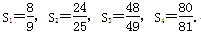
观察上述结果,推测出Sn(n∈N*),并用数学归纳法加以证明.
推测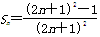 (n∈N*).用数学归纳法证明如下:
(n∈N*).用数学归纳法证明如下:
(1)当n=1时,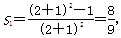 ,等式成立;
,等式成立;
(2)假设当n=k时,等式成立,
即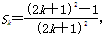 那么当n=k+1时,
那么当n=k+1时,
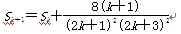

也就是说,当n=k+1时,等式成立.
根据(1)和(2),可知对一切n∈N*,等式均成立.
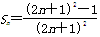 (n∈N*).用数学归纳法证明如下:
(n∈N*).用数学归纳法证明如下:(1)当n=1时,
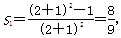 ,等式成立;
,等式成立;(2)假设当n=k时,等式成立,
即
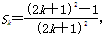 那么当n=k+1时,
那么当n=k+1时,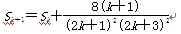

也就是说,当n=k+1时,等式成立.
根据(1)和(2),可知对一切n∈N*,等式均成立.
略

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
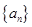 是首项为23,公差为整数的等差数列,且
是首项为23,公差为整数的等差数列,且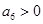 ,
,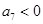 .
.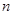 项和
项和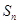 的最大值;
的最大值;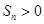 时,求
时,求 }的前n项和Sn= —a
}的前n项和Sn= —a )
)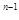 +2 (n为正整数).
+2 (n为正整数). =
= .,并求数列{a
.,并求数列{a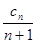 =
=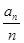 ,T
,T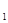 +c
+c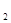 +···+c
+···+c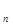 .
.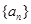 ,若点
,若点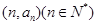 在经过点(5,3)的定直线
在经过点(5,3)的定直线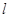 上,则数列
上,则数列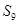 =( )
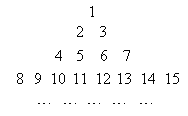
=( ) 行共有
行共有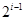 个正整数,设
个正整数,设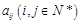 表示位于这个数表中从上往下数第
表示位于这个数表中从上往下数第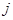 个数.
个数.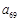 的值;
的值;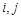 表示
表示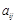 ;
;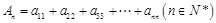 ,求证:当
,求证:当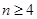 时,
时,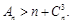
 f(a1),f(
f(a1),f( a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列. 出m的范围;若不存在,请说明理由.
出m的范围;若不存在,请说明理由.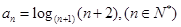 ,我们把使乘积
,我们把使乘积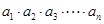 为整数的数
为整数的数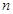 叫做“劣数”,则在区间
叫做“劣数”,则在区间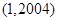 内的所有劣数的和为
内的所有劣数的和为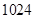
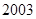
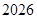
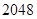
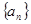 的通项公式
的通项公式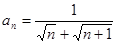 ,则该数列的前( )项之和等于
,则该数列的前( )项之和等于




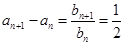 (n="1," 2, 3,……),cn=anbn, 试求
(n="1," 2, 3,……),cn=anbn, 试求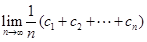 (12分)
(12分)