题目内容
(本小题满分12分)
已知数列{a }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)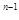 +2 (n为正整数).
+2 (n为正整数).
(1)证明:a =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项
(2)若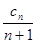 =
=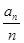 ,T
,T = c
= c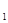 +c
+c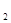 +···+c
+···+c ,求T
,求T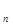 .
.
已知数列{a
 }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)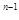 +2 (n为正整数).
+2 (n为正整数).(1)证明:a
 =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项(2)若
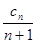 =
=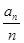 ,T
,T = c
= c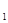 +c
+c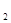 +···+c
+···+c ,求T
,求T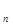 .
.⑴a =
=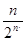 . ⑵T
. ⑵T =3—
=3—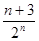 .
.
 =
=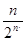 . ⑵T
. ⑵T =3—
=3—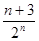 .
. 本试题主要是考查了数列通项公式的求解以及数列的求和的综合运用。
(1)因为数列{a }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)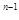 +2 (n为正整数).
+2 (n为正整数).
利用前n项和与通项公式的 关系得到a =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项
(2)根据第一问得到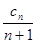 =
=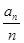 ,然后运用错位相减法得到数列的和式。
,然后运用错位相减法得到数列的和式。
解:⑴由S = —an—(
= —an—( )
)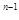 +2,得S
+2,得S = —a
= —a —(
—( )
) +2,两式相减,得a
+2,两式相减,得a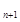 =
=
—a + a
+ a +(
+( )
) ,即a
,即a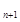 =
= a
a +(
+( )
)
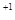 .---------------------------------------2分
.---------------------------------------2分
因为S = —a
= —a —(
—( )
)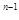 +2,令n=1,得a
+2,令n=1,得a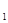 =
= .对于a
.对于a =
= a
a +(
+( )
)
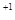 ,两端同时除以(
,两端同时除以( )
)
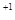 ,得2
,得2 a
a =2
=2 a
a +1,即数列{2
+1,即数列{2 a
a }是首项为2
}是首项为2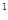 ·a
·a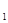 =1,公差为1的等差数列,故2
=1,公差为1的等差数列,故2 a
a =n,所以a
=n,所以a =
=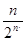 .------------------------------------6分
.------------------------------------6分
⑵由⑴及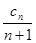 =
=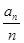 ,得c
,得c = (n+1)(
= (n+1)( )
) ,
,
所以T =2×
=2× +3×(
+3×( )
)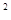 +4×(
+4×( )
)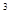 +···+(n+1) (
+···+(n+1) ( )
) ,①
,①
 T
T =2×(
=2×( )
)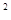 +3×(
+3×( )
)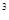 +4×(
+4×( )
)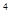 +···+(n+1) (
+···+(n+1) ( )
) ,②
,②
由①—②,得
 T
T =1+(
=1+( )
)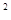 +(
+( )
)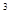 +···+(
+···+( )
) -(n+1) (
-(n+1) ( )
) =1+
=1+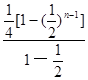 —
—
(n+1) ( )
) =
=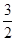 —
—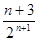 . 所以T
. 所以T =3—
=3—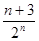 .------------------------------------12分
.------------------------------------12分
(1)因为数列{a
 }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)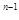 +2 (n为正整数).
+2 (n为正整数).利用前n项和与通项公式的 关系得到a
 =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项(2)根据第一问得到
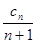 =
=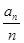 ,然后运用错位相减法得到数列的和式。
,然后运用错位相减法得到数列的和式。解:⑴由S
 = —an—(
= —an—( )
)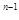 +2,得S
+2,得S = —a
= —a —(
—( )
) +2,两式相减,得a
+2,两式相减,得a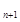 =
=—a
 + a
+ a +(
+( )
) ,即a
,即a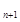 =
= a
a +(
+( )
)
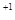 .---------------------------------------2分
.---------------------------------------2分因为S
 = —a
= —a —(
—( )
)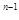 +2,令n=1,得a
+2,令n=1,得a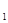 =
= .对于a
.对于a =
= a
a +(
+( )
)
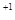 ,两端同时除以(
,两端同时除以( )
)
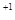 ,得2
,得2 a
a =2
=2 a
a +1,即数列{2
+1,即数列{2 a
a }是首项为2
}是首项为2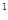 ·a
·a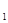 =1,公差为1的等差数列,故2
=1,公差为1的等差数列,故2 a
a =n,所以a
=n,所以a =
=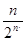 .------------------------------------6分
.------------------------------------6分⑵由⑴及
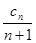 =
=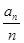 ,得c
,得c = (n+1)(
= (n+1)( )
) ,
,所以T
 =2×
=2× +3×(
+3×( )
)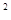 +4×(
+4×( )
)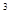 +···+(n+1) (
+···+(n+1) ( )
) ,①
,① T
T =2×(
=2×( )
)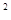 +3×(
+3×( )
)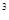 +4×(
+4×( )
)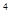 +···+(n+1) (
+···+(n+1) ( )
) ,②
,②由①—②,得
 T
T =1+(
=1+( )
)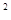 +(
+( )
)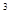 +···+(
+···+( )
) -(n+1) (
-(n+1) ( )
) =1+
=1+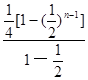 —
—(n+1) (
 )
) =
=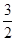 —
—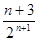 . 所以T
. 所以T =3—
=3—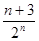 .------------------------------------12分
.------------------------------------12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
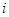 行第
行第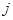 列的数为
列的数为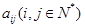 ,则:
,则: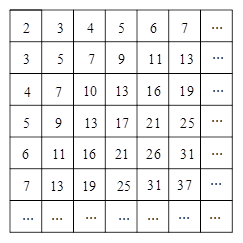
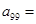 ; (Ⅱ)表中数
; (Ⅱ)表中数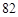 共出现 次.
共出现 次.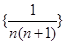 的前
的前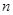 项和为
项和为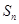 ,则
,则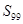 等于
等于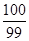
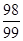
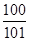
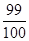
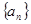 的前n次之和为
的前n次之和为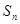 满足
满足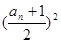
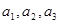 ,
,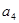 ②猜测数列
②猜测数列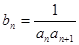 ,数列
,数列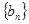 的前n项和为
的前n项和为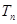 ,求
,求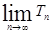 的值.
的值.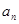 }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;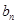 }满足:
}满足: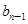 =
=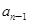 (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.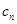 =
=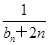 (n∈N﹡),若{
(n∈N﹡),若{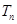 ,求
,求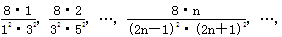 Sn为该数列的前n项和,计算得
Sn为该数列的前n项和,计算得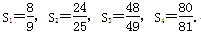
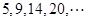 为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即
为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即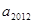 -5= .
-5= .


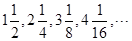 前n项的和为()
前n项的和为()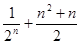
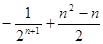
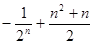
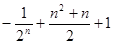
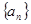 的前
的前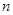 项和
项和 满足
满足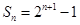 ,则通项公式为 .
,则通项公式为 .