题目内容
(本小题满分13分)
已知f(x)=mx(m为常数,m>0且m≠1).
设 f(a1),f(
f(a1),f( a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
(1)求证:数列{an}是等差数列;
(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;
(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,
求 出m的范围;若不存在,请说明理由.
出m的范围;若不存在,请说明理由.
已知f(x)=mx(m为常数,m>0且m≠1).
设
 f(a1),f(
f(a1),f( a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.
a2),…,f(an)…(n∈N?)是首项为m2,公比为m的等比数列.(1)求证:数列{an}是等差数列;
(2)若bn=an·f(an),且数列{bn}的前n项和为Sn,当m=2时,求Sn;
(3)若cn=f(an)lgf(an),问是否存在m,使得数列{cn}中每一项恒小于它后面的项?若存在,
求
 出m的范围;若不存在,请说明理由.
出m的范围;若不存在,请说明理由.解:(1)由题意f(an)=m2·mn+1,即man,=mn+1.
∴an=n+1,(2分) ∴an+1-an=1,
∴数列{an}是以2为首项,1为公差的等差数列.(4分)
(2)由题意bn=anf(an)=(n+1)·mn+1,
当m=2时,bn=(n+1)·2n+1
∴Sn=2·22+3·23+4·24+…+(n+1)·2n+1 ①(6分)
①式两端同乘以2,得
2Sn=2·23+3·24+4·25+…+n·2n+1+(n+1)·2n+2 ②
②-①并整理,得

略

练习册系列答案
相关题目
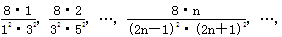 Sn为该数列的前n项和,计算得
Sn为该数列的前n项和,计算得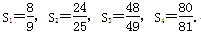
 中,
中,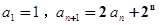
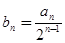 ,证明:数列
,证明:数列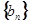 是等差数列。
是等差数列。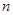 项和
项和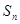 。
。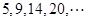 为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即
为“梯形数列”.根据图形的构成,此数列的第2012项与5的差,即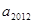 -5= .
-5= .


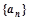 的首项为
的首项为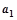 ,公差为
,公差为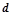 ,前
,前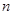 项的和为
项的和为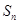 ,则数列
,则数列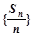 为等差数列,且通项为
为等差数列,且通项为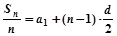 。类似地,请完成下列命题:若各项均为正数的等比数列
。类似地,请完成下列命题:若各项均为正数的等比数列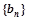 的首项为
的首项为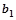 ,公比为
,公比为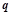 ,前
,前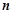 项的积为
项的积为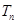 ,则数列 。
,则数列 。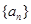 前
前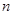 项和为
项和为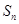 ,若
,若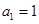 ,
,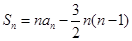 .
.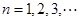
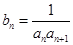 ,数列
,数列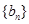 前
前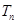 ,证明:
,证明: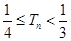 ;
;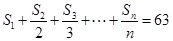 ?若存在,求出
?若存在,求出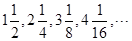 前n项的和为()
前n项的和为()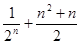
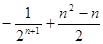
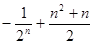
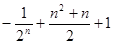
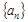 的通项公式是
的通项公式是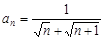 ,若前n项的和为10,则项数n为( )
,若前n项的和为10,则项数n为( )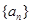 满足性质“对任意正整数
满足性质“对任意正整数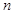 ,
,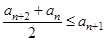 都成立”且
都成立”且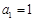 ,
,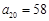 ,则
,则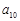 的最小值为
的最小值为