Question

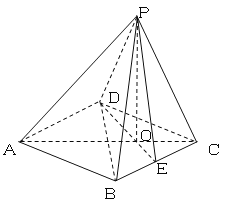
【题目】如图，已知四棱锥P－ABCD的底面是边长为2的菱形，∠BCD＝60°，点E是BC边

的中点，AC，DE交于点O，，且PO⊥平面ABCD.

（1）求证：PD⊥BC；

（2）在线段AP上找一点F，使得BF∥平面PDE，并求此时四面体PDEF的体积．

Answer 1

【答案】(1)证明见解析.

(2) VP-BDE=1.

【解析】

(1)先证明BC⊥平面PDE，即证PD⊥BC.（2）取AP中点为F，再取PD中点为G，连结FG，再证明FG⊥平面PDE，最后求四面体PDEF的体积．

（1）由题可得△BCD为正三角形，E为BC中点，故DE⊥BC.

又PO⊥平面ABCD，BC平面ABCD，则PO⊥BC，

而DE∩PO＝O，平面，

所以BC⊥平面PDE.

又PD平面PDE，故PD⊥BC.

（2）取AP中点为F，再取PD中点为G，连结FG.

则FG为△PAD中位线，故FG AD，

又BE AD，所以FGBE，于是四边形BFGE为平行四边形，

因此BF∥EG.又BF平面PDE，EG平面PDE,

所以BF∥平面PDE.

由（1）知，BC⊥平面PDE.则有BC⊥PE，BC⊥DE，

而BC∥FG，故FG⊥PE，FG⊥DE，且DE∩PE＝E，

所以FG⊥平面PDE.

于是四面体PDEF的体积为V=S△PDE·FG＝××2××1＝1.