��Ŀ����
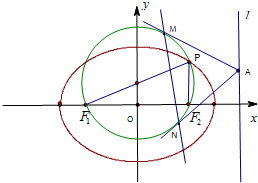
��ͼ����ԲC��
+
=1��a��b��0���Ķ���ΪA1��A2��B1��B2������ΪF1��F2��|A1B2|=
��S?A1B1A2B2=2S?B1F1B2F2
��������ԲC�ķ��̣�
������ֱ��m��Q��1��1����������Բ�ཻ��M��N���㣬��Q��MN���е�ʱ����ֱ��m�ķ��̣�
������nΪ��ԭ���ֱ�ߣ�l����n��ֱ�ཻ��P��������Բ�ཻ������A��B��ֱ�ߣ�|
|=1���Ƿ��������ֱ��lʹ��ABΪֱ����Բ��ԭ�㣿�����ڣ����ֱ��l�ķ��̣��������ڣ���˵�����ɣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
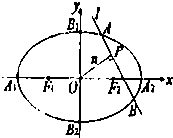
��������ԲC�ķ��̣�
������ֱ��m��Q��1��1����������Բ�ཻ��M��N���㣬��Q��MN���е�ʱ����ֱ��m�ķ��̣�
������nΪ��ԭ���ֱ�ߣ�l����n��ֱ�ཻ��P��������Բ�ཻ������A��B��ֱ�ߣ�|
| OP |

������������|A1B2|=
=
��a2+b2=7����1�֣�
����S��A1B1A2B2=2S��B1F1B2F2����2a•b=2•2c•b����a=2c����2�֣�
���a2=4��b2=3������3�֣���
����ԲC�ķ���Ϊ
+
=1������4�֣�
����ֱ��m��б�ʴ���ʱ����ֱ��m�ķ���Ϊy=k��x-1��+1��M��x1��y1����N��x2��y2����
��
+
=1��
+
=1��
��ʽ����ã�k=
=-
��
��
��Q��MN���е㣬
��ɵ�ֱ��m��б��Ϊk=
=-
����7�֣�
��ֱ��m��б�ʲ�����ʱ����x=1������Բ���̲����M(1��
)��N(1��-
)��
��ʱMN���е�Ϊ��1��0����
��x=1����������Ҫ����8�֣�
���ϣ�ֱ��m�ķ���Ϊ3x+4y-7=0����9�֣�
������A��B���������ֱ�Ϊ��x1��y1������x2��y2�����������������ֱ��l���ڣ�
��i����l����ֱ��x��ʱ����l�ķ���Ϊy=kx+m����l��n��ֱ�ཻ��P����|
|=1��
=1����m2=k2+1������10�֣�
�֡���ABΪֱ����Բ��ԭ�㣬��OA��OB����x1x2+y1y2=0��
��y=kx+m������Բ���̣��ã�3+4k2��x2+8kmx+��4m2-12��=0��
�������ʽ�ɵ�x1+x2=
����x1x2=
����
0=x1x2+y1y2=x1x2+��kx1+m����kx2+m��=x1x2+k2x1x2+km(x1+x2)+m2=(1+k2)x1x2+km(x1+x2)+m2��
���ܣ��ݴ�����ʽ������ã�1+k2����4m2-12��-8k2m2+m2��3+4k2��=0����
��m2=1+k2����������-5��k2+1��=0��ì�ܣ�
����ʱֱ��l�����ڣ�����12�֣�
��ii����l��ֱ��x��ʱ������|
|=1��ֱ��l�ķ���Ϊx=1��x=-1��
��A��B�����������1��
������1��-
����-1��
������-1��-
����
��x=1ʱ��
•
=��1��
��•��1��-
��=-
��0��
��x=-1ʱ��
•
=��-1��
��•��-1��-
��=-
��0��
���ʱֱ��lҲ�����ڣ�
����������ʹ
•
=0������ֱ��l����������������ֱ��lʹ��ABΪֱ����Բ��ԭ�㣮
| a2+b2 |
| 7�� |
����S��A1B1A2B2=2S��B1F1B2F2����2a•b=2•2c•b����a=2c����2�֣�
���a2=4��b2=3������3�֣���
����ԲC�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
����ֱ��m��б�ʴ���ʱ����ֱ��m�ķ���Ϊy=k��x-1��+1��M��x1��y1����N��x2��y2����
��
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
��ʽ����ã�k=
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| x1+x2 |
| y1+y2 |
��Q��MN���е㣬
��ɵ�ֱ��m��б��Ϊk=
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
��ֱ��m��б�ʲ�����ʱ����x=1������Բ���̲����M(1��
| 3 |
| 2 |
| 3 |
| 2 |
��ʱMN���е�Ϊ��1��0����
��x=1����������Ҫ����8�֣�
���ϣ�ֱ��m�ķ���Ϊ3x+4y-7=0����9�֣�
������A��B���������ֱ�Ϊ��x1��y1������x2��y2�����������������ֱ��l���ڣ�
��i����l����ֱ��x��ʱ����l�ķ���Ϊy=kx+m����l��n��ֱ�ཻ��P����|
| OP |
| |m| | ||
|
�֡���ABΪֱ����Բ��ԭ�㣬��OA��OB����x1x2+y1y2=0��
��y=kx+m������Բ���̣��ã�3+4k2��x2+8kmx+��4m2-12��=0��
�������ʽ�ɵ�x1+x2=
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
0=x1x2+y1y2=x1x2+��kx1+m����kx2+m��=x1x2+k2x1x2+km(x1+x2)+m2=(1+k2)x1x2+km(x1+x2)+m2��
���ܣ��ݴ�����ʽ������ã�1+k2����4m2-12��-8k2m2+m2��3+4k2��=0����
��m2=1+k2����������-5��k2+1��=0��ì�ܣ�
����ʱֱ��l�����ڣ�����12�֣�
��ii����l��ֱ��x��ʱ������|
| OP |
��A��B�����������1��
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
��x=1ʱ��
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
��x=-1ʱ��
| OA |
| OB |
| 3 |
| 2 |
| 3 |
| 2 |
| 5 |
| 4 |
���ʱֱ��lҲ�����ڣ�
����������ʹ
| OA |
| OB |

��ϰ��ϵ�д�
�����Ŀ