题目内容

已知椭圆C：
x2
a2
+
y2
b2
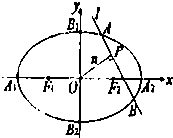
=1（a＞b＞0），左、右两个焦点分别为F1、F2，上顶点M（0，b），△MF1F2为正三角形且周长为6，直线l：x=my+4与椭圆C相交于A、B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
OA
•
OB
的取值范围．
（Ⅰ）∵上顶点M（0，b），△MF1F2为正三角形且周长为6，
∴a=2，c=1，b=
3
，
∴椭圆的方程为
x2
4
+
y2
3
=1；
（Ⅱ）直线l：x=my+4代入椭圆方程，得（3m2+4）y2+24my+36=0，
由△=（24m）2-4×36×（3m2+4）＞0
可得m2＞4．
设A（x1，y1），B（x2，y2），
则y1+y2=-
24m
3m2+4
，y1y2=
36
3m2+4

∴
OA
•
OB
=x1x2+y1y2=（m2+1）y1y2+4m（y1+y2）+16=-4+
116
3m2+4
，
∵m2＞4，
∴3m2+4＞16，
∴
OA
•
OB
∈（-4，
13
4
）．
练习册系列答案
相关题目
已知中心在原点，焦点在x轴上的椭圆焦距为2，离心率为
1
2

（1）求椭圆的标准方程
（2）若直线l过点（1，2）且倾斜角为45°且与椭圆相交于A，B两点，求弦长|AB|．
椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1（-1，0）、F2（1，0），O是坐标原点，C的右顶点和上顶点分别为A、B，且△AOB的面积为
5
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点P（4，0）作与x轴不重合的直线l与C交于相异两点M、N，交y轴于Q点，证明
|PQ|
|PM|
+
|PQ|
|PN|
为定值，并求这个定值．
已知F1，F2是椭圆
x2
16
+
y2
9
=1的两焦点，过点F2的直线交椭圆于A，B两点，在△AF1B中，若有两边之和是10，则第三边的长度为______．
已知椭圆M：
x2
a2
+
y2
b2
=1(a＞b＞0)经过如下五个点中的三个点：P1(-1，-
2
2
)，P2（0，1），P3(
1
2
，
2
2
)，P4(1，
2
2
)，P5（1，1）．
（Ⅰ）求椭圆M的方程；
（Ⅱ）设点A为椭圆M的左顶点，B，C为椭圆M上不同于点A的两点，若原点在△ABC的外部，且△ABC为直角三角形，求△ABC面积的最大值．
已知双曲线的方程为5x2-4y2=20两个焦点为F1，F2．
（1）求此双曲线的焦点坐标和渐近线方程；
（2）若椭圆与此双曲线有共同的焦点，且有一公共点P满足|PF1|•|PF2|=6，求椭圆的方程．
如图，直线l：y=x+b与抛物线x2=4y相切于点A．
（1）求实数b的值；
（2）若过抛物线的焦点且平行于直线l的直线l1交抛物线于B，C两点，求△ABC的面积．
如图，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的顶点为A1，A2，B1，B2，焦点为F1，F2，|A1B2|=
7
，S?A1B1A2B2=2S?B1F1B2F2
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线m过Q（1，1），且与椭圆相交于M，N两点，当Q是MN的中点时，求直线m的方程．
（Ⅲ）设n为过原点的直线，l是与n垂直相交于P点且与椭圆相交于两点A，B的直线，|
OP
|=1，是否存在上述直线l使以AB为直径的圆过原点？若存在，求出直线l的方程；若不存在，请说明理由．
曲线y=x2上的点到直线2x+y+4=0的最短距离是（　　）
A．
5
5
B．
2
5
5
C．
3
5
5
D．
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网